Highlights

  • A Reinforced Cross-Modal Matching (RCM) framework to learn global matching between natural language instructions and trajectories using extrinsic and intrinsic rewards
  • State of the art performance of the Room2Room (R2R) dataset on a Vision-Language Navigation (VLN) challenge
  • A Self-Supervised Imitation Learning (SIL) method for exploration of unseen environments

Introduction

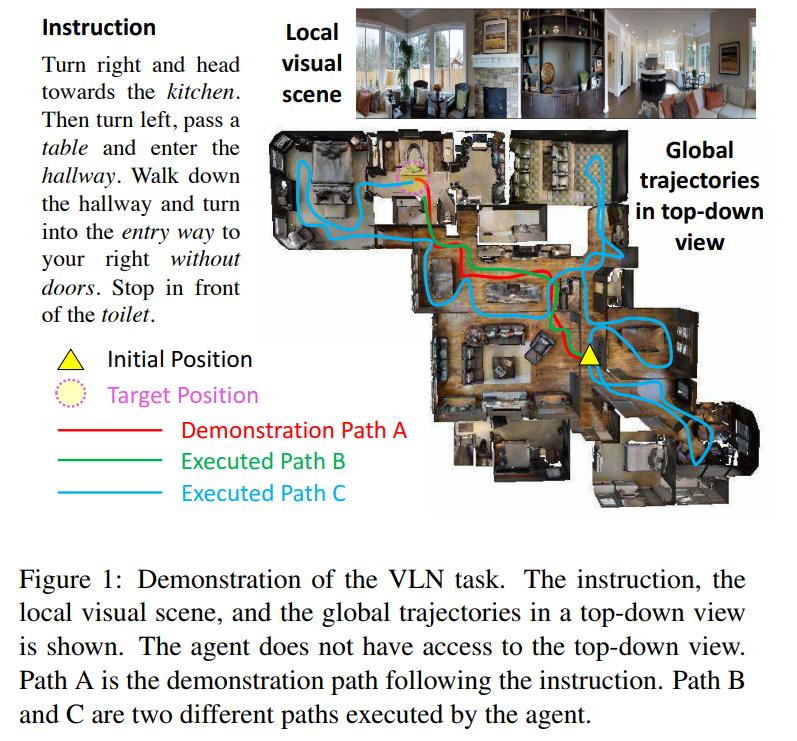
VLN is the task of navigating in a 3D environment based on natural language inputs. VLN is especially challenging as the agent must learn a good representation of the 3D input, the text instructions and the link between the two. Also, feedback tends to be really sparse as success is only determined if the agents reaches the destination, whether or not it followed the instructions. Furthermore, a trajectory might receive no feedback if the agent followed the instructions correctly but stopped short of where it should have.

Methods

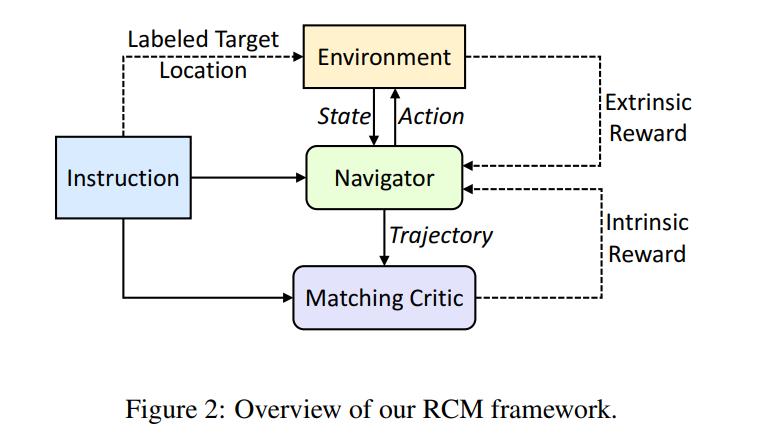
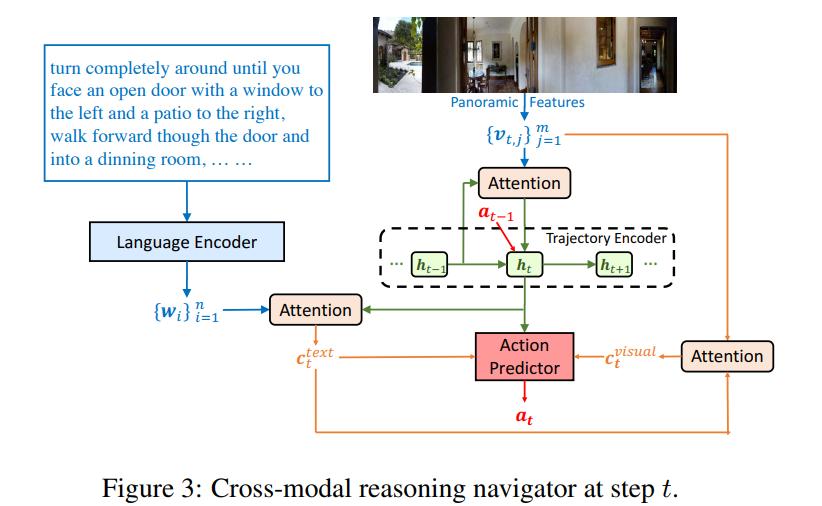
First, the authors introduce the Cross-Modal Reasoning Navigator, which is the policy of the agent. The observation the agent receives is a first-person panoramic view split into \(m\) patches, run through a pre-trained CNN giving features \(v\) s.t. \(\{v_{t,j}\}^m_{j=1}\) at viewpoint \(j\).

The trajectories are then encoded as the hidden states \(h_t\) of an LSTM s.t

\[h_t = LSTM([v_t,a_{t-1}],h_{t-1}\]

where \(a\) is the action taken and \(v\) is augmented with attention

\[v_t = \sum_j{\alpha_{t,j}v_{t,j}} = \sum_j{softmax(h_{t-1}W_h(v_{t,j}W_v)^T)v_{t,j}} = attention(h_{t-1}, \{v_{t,j}\}^m_{j=1})\]

where \(W\) are learnable attention maps and \(\alpha\) the attention weights over the features.

The authors also learn the textual context conditioned on the visual inputs by encoding the language instructions into textual features \(w\) s.t. \(\{w_{t,i}\}^m_{i=1}\) and compute the textual context as

\[c_t^{text} = attention(h_t,\{w_{t,i}\}^m_{i=1})\]

To help the agent know where to look, the authors also learn the visual context conditioned on the textual context as

\[c_t^{visual} = attention(c_t^{text},\{v_{t,j}\}^m_{j=1})\]

Finally, the action is predicted by

\[p_k = softmax([h_t,c_t^{text},c_t^{visual}]W_c(u_kW_u)^T)\]

where \(p_k\) is the probability of the navigable direction, \(u_k\) the action embedding obtained by concatenating a 4-dimensional orientation feature vector \([sin\psi,cos\psi,sin\omega,cos\omega]\) and the visual features associated with the direction.

Figure 3 sums up the action-decision process.

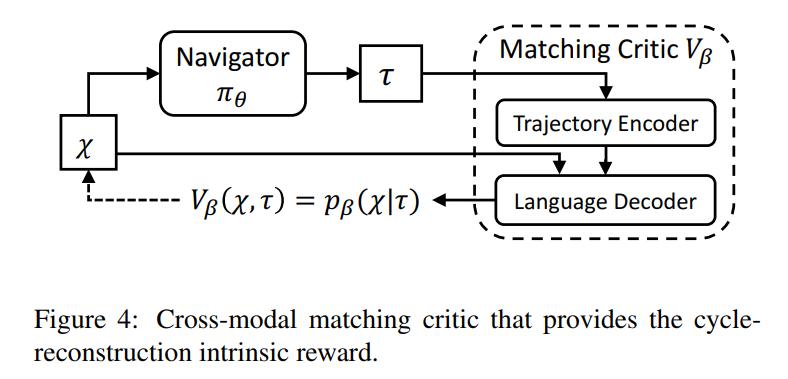
In addition to the extrinsic reward given by the environment, the authors also derive an intrinsic reward provided by a Cross-Modal Matching Critic

\[R_{intr} = V_{\beta}(\mathcal{X},\tau) = V_{\beta}(\mathcal{X},\pi_\Theta(\mathcal{X}))\]

where \(\mathcal{X}\) are the textual instructions and \(\tau\) the trajectory. One way to reward the agent is to try to maximize the probability of reconstructing a set of instructions given a trajectory. The higher the probability is, the better the produced trajectory is aligned with the instructions.

\(V_\beta\) then becomes a sequence-to-sequence language model, which encodes the trajectory \(\tau\) and produces the probability distributions of generating each word of \(\mathcal{X}\) with the language decoder:

\[R_{intr} = p_{\beta}(\mathcal{X}|\pi_\Theta(\mathcal{X})) = p_{\beta}(\mathcal{X}|\tau)\]

To speed up the training process, the critic is pretrained with human demonstrations via supervised-learning.

The authors then used the REINFORCE algorithm to train their model, with the following gradient:

\[\nabla_{\theta}\mathcal{L}_{rl} = -A_t\nabla_{\theta}log\pi_\theta(a_t|s_t)\]

where the advantage function \(A = R_{extr} + {\delta}R_{intr}\) and \(R_{extr}\) a reward function based on the distance to the objective and a bonus at the last time step if the agent reaches the objective.

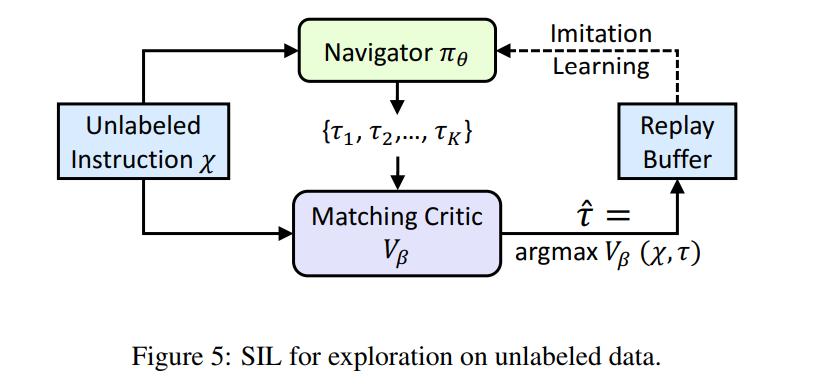
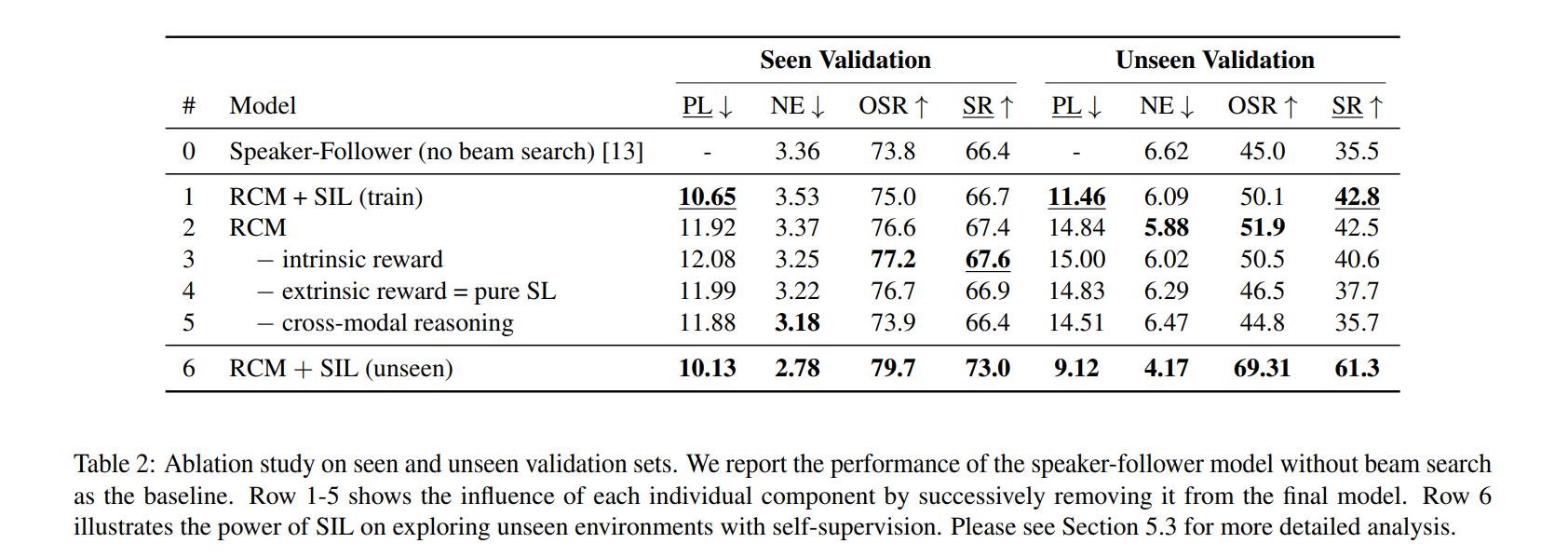
Finally, a common part of VLN is to test the agents on unseen environments. To help with this, the authors propose SIL, a method for imitating the agent’s past good decisions. Simply put, given a set of instructions \(\mathcal{X}\), the agent produces a set of trajectories and then stores the best \(\hat{\tau}\) according to the Matching Critic. Because the target is unknown and the rewards come from the agent, the process can be seen as self-supervised. The loss for SIL then becomes

\[L_{sil} = -R_{intr}log\pi_\theta(a_t|s_t)\]

Data

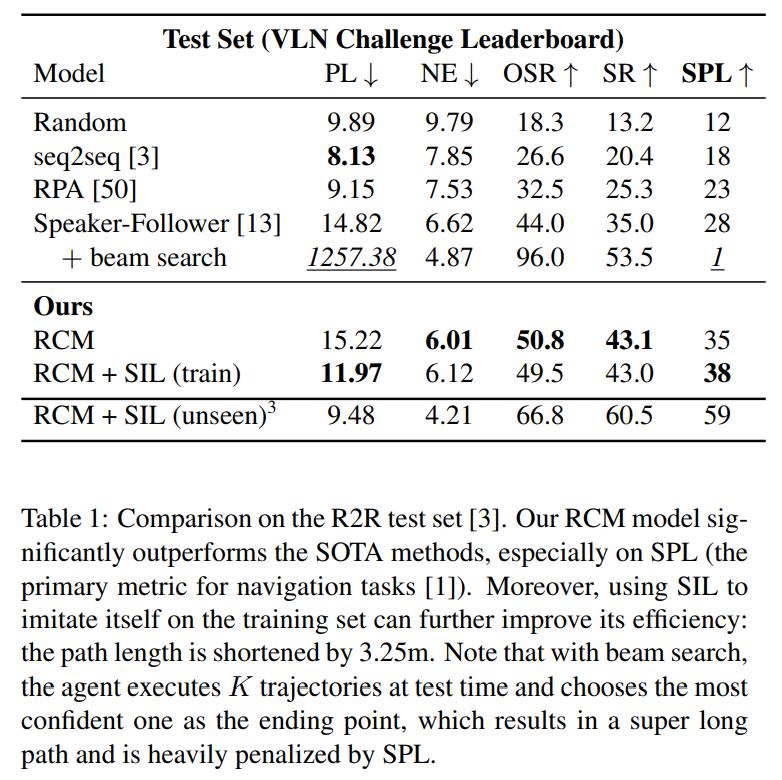
The R2R dataset consists of 7 189 paths and 21 567 human-annotated instructions with an average length of 29 words. The dataset is separated into seen and unseen environments, the latter being used for testing purposes.

Five evaluation metrics were used:

  • PL: Path length, the total length of the executed path
  • NE: Navigation Error, the shortest-path distance between the agent’s final position and the target
  • OSR: Oracle Success Rate, the success rate at the closest point to the goal that the agent has visited along the trajectory
  • SR: Sucess Rate, the percentage of predicted end-locations within 3m of the target locations
  • SPL: Success Rate rated by inverse Path Length, trades-off Success Rate against Path Length

Results