Continuous Dice Coefficient: a Method for Evaluating Probabilistic Segmentations
Highlights
Authors propose to use a variant of the Dice coefficient to evaluate continuous/probabilistic segmentations.
Introduction
Overlapping measures are often utilized to quantify the similarity between two binary regions. However, modern segmentation algorithms output a probability or confidence map with continuous values in the zero-to-one interval. These maps have to be binarized/thresholded to use the Dice coefficient.
Also, it has been shown that the Dice coefficient is directly related to structure’s size: the smaller the structure the lower the Dice coefficient (given a fixed resolution). Therefore, Dice is a difficult measure for comparing methods tested on different structures.
Authors extend the definition of the classical Dice coefficient (DC) overlap to facilitate the direct comparison of a ground truth binary image with a probabilistic map. They call the extended method continuous Dice coefficient (cDC).
Methods
Classical Dice coefficient \(DC := \frac{2 \lvert A \cap B \rvert}{\lvert A \rvert + \lvert B \rvert}\)
The classical DC fails to incorporate the probabilistic information and counts all errors/inaccuracies equally.
The proposed score cDC score: \(cDC := \frac{\lvert A \cap B \rvert}{c\lvert A \rvert + \lvert B \rvert}\)
where \(c\) is defined as the mean value of B over the voxels where both A and B are positive: \(c = \frac{\sum_{i} a_{i} b_{i}}{\sum_{i} a_{i} sign(b_{i})}\) and \(sign(x)\) is defined as \(sign(x) = { \begin{cases} 1 &\; \text{if}\; x > 0\\ 0 &\; \text{if}\; x = 0\\ -1 &\; \text{if}\; x < 0 \end{cases} }\)
If \(\sum_{i} a_{i} sign(b_{i} = 0\) (no overlap between A and B), authors arbitrary define \(c = 1\). cDC will be zero in that case.
When \(b \in {0,1}\), (i.e., a binary value) \(c = 1\) and \(cDC = DC\), and thus cDC is a consistent extension of DC.
Properties:
- \(cDC \leq 1\) and \(cDC = 1\) iff overlap is complete.
- cDC is monotonically decreasing with the amount of overlap.
Data
Authors used gold-standard segmentations of the right subthalamic nucleus (STN), globus pallidus (GP), and thalamus on high-resolution 7T MRI brain images of a cohort of 46 Parkinsons’ disease patients to evaluate their method.
A threshold of 0.1 was applied to the segmentation probabilistic map to convert it into a binary image and compute the DC. This threshold was selected to achieve maximal DC value.
Results

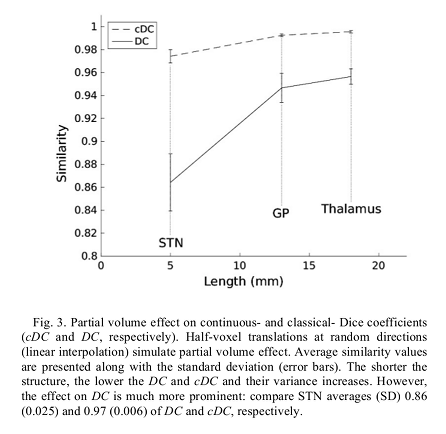
Conclusions
The cDC is well defined for probabilistic segmentation, less biased to the structure’s size and more robust to partial volume effects in comparison to DC.
Authors argue that as a better measurement tool, the method opens the door for the development of better segmentation methods.
Remarks
It seems unclear how \(b_{i}\) can be negative so that \(sign(x)\) can take the value -1.
The described properties seem to be in contradiction.
A very limited set of experiments were performed.
The impact or benefit of the new score remains to be evaluated.