Introduction

This is my “best paper” of the CVPR 2019 edition. It revisits the notion of robust regression loss function \(\rho(.)\),

\[\arg \min_\theta \rho \left( f_\theta(x)-y \right )\]

as it proposes a new general loss function which is a superset of many existing losses. The parameters of this loss can be automatically adapted to fit the true nature of the problem.

Methods

\(\rho(.)\) can be an L2 or an L1 function. However, it can also be a robust function like a Welsch loss, a Geman-McClure loss, or a Cauchy loss. The author shows that all these functions are special cases of a more general fobust function

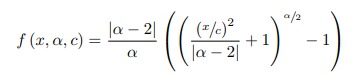
where \(\alpha\) is a shape parameter. By playing with \(\alpha\), one can recover the various loss functions mentioned before.

Although \(\alpha\) can be seen as an extra hyperparameter that needs to be tuned, one can define it as a trainable parameter. To do so, the author encapsulates the loss into a PDF formulation:

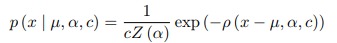
where

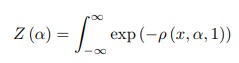
so the optimization function becomes

\[\arg \min_{\theta,\alpha} -log(p(x|\alpha) = \rho \left( x,\alpha \right ) + log(Z(\alpha))\]

where \(log(Z(\alpha))\) is some complicated analytical function which the author approximates with a cubic spline function.

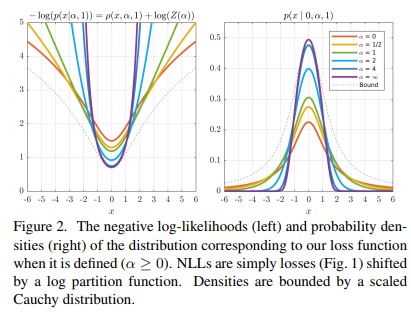
Having \(Z(.)\) in the loss function is important because without it, the system would trivially minimize the cost of outliers by setting \(\alpha\) to be as small as possible. However, as shown in Fig.2, reducing \(\alpha\) will decrease the loss of outlisers but will increase the loss of inliers.

Results

Results are quite convincing on various applications like VAEs

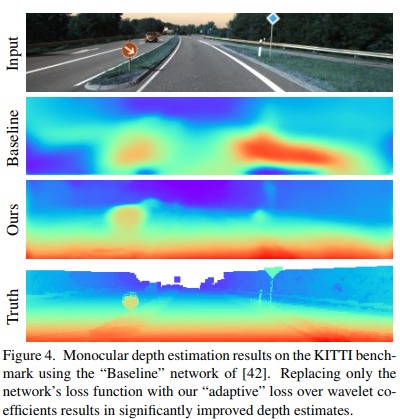
and monocular depth estimation

Video

The author recorded a nice video. Don’t miss it!