Highlights

Authors propose a deep learning method, which they call DeepBundle, for registration- and atlas-free fiber parcellation.

The method uses graph convolution neural networks (GCNNs) to predict the parcellation label of each fiber tract.

Their results show an improvement over RecoBundles.

Introduction

Tract-based analysis (TBA) on diffusion Magnetic Resonance Images (dMRI) requires methods for segmenting whole-brain tractograms into fiber bundles.

Existing fiber parcellation approaches can be divided into two categories:

• ROI-based approaches first parcellate the brain surface based on an atlas and then use the parcellation ROIs to extract different fiber bundles.
• Streamline-based approaches employ streamline registration methods to directly transfer the fiber parcellation information from an atlas to tractograms of an individual.

These methods are directly affected by registration accuracy, and registration is a time-consuming task.

Wasserthal et al. ¹ proposed to predict the binary mask of a fiber bundle from the whole brain fiber peaks using convolutional neural networks. This method avoids the registration procedure but is limited to generating a binary tract segmentation mask rather than the parcellation labels of the fiber tracts.

Authors propose a convolutional neural network-based, registration-free method to outputs bundle labels.

Methods

Authors propose a graph convolutional neural networks (GCNN) that considers the coordinates of the points on each fiber tract as functions defined on a graph. The graph is said to encode the geometric relationship between the sampling points of the each streamline.

Spectral graph convolution ² is used to extract the underlying latent geometric features of each fiber tract. The spectral graph convolution notion generalizes conventional convolution in Euclidean space using graph Fourier transformation.

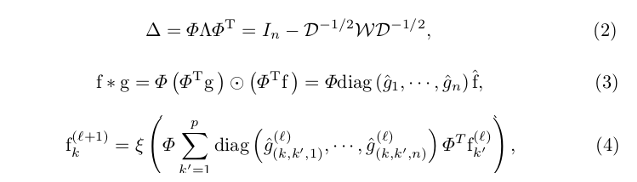
where (2) is the eigendecomposition of the graph Laplacian: \(\Phi\) is the matrix of eigenvectors and \(\Lambda\) is the diagonal matrix of eigenvalues; \(\mathfrak{W}\) is the binary adjacency matrix, and \(\mathfrak{D} = \sum_{j \neq i} w_{(i,j)}\) is the degree matrix.

The eigenvectors can be interpreted as the Fourier bases, and \(\Phi^{T}\) is used to transform features from the spatial domain to the spectral domain.

(3) gives the graph Fourier transform: \(f\) is the input signal of geometric features of one streamline; \(g\) is a convolutional filter in the spatial domain; \(diag(\hat{g}_{1}, \cdots, \hat{g}_{n}\) is the spectral domain convolutional filter.

(4) summarizes the GCNN operation in a layer, being \(\xi\) the non-linearity.

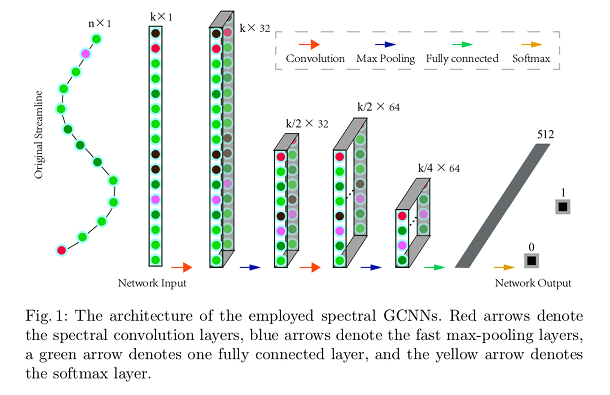
Authors use separately trained networks for segmenting different fiber bundles from the whole-brain tracts.

During the testing stage, the point coordinates extracted from fiber tracts of the tractogram are directly fed to the trained networks.

Data

HCP fiber tract dataset: 105 subjects, each with 72 fiber bundles.

Randomnly selected 25 subjects for training, 2 for validation, and 11 for testing.

Results

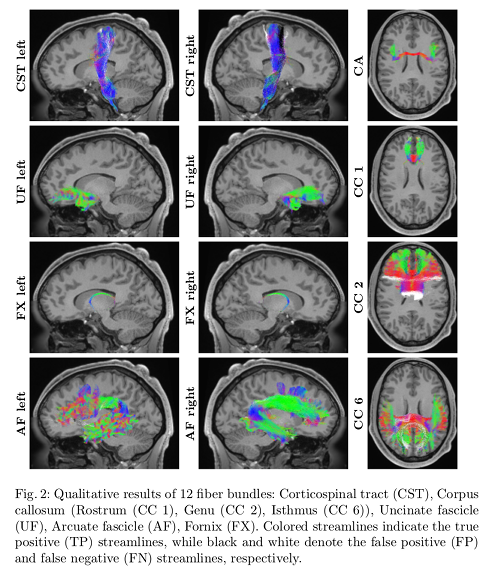
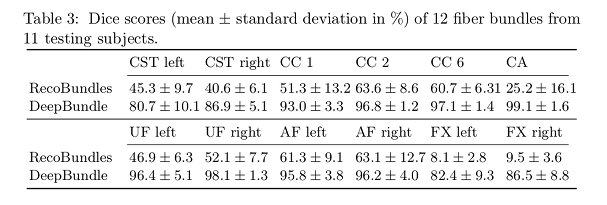
• DeepBundle yields high precision and high recall values for the bundles studied.
• Lower scores in CST are attributed to misclassification arising from the similarities streamlines in the CST may have with neighboring bundles.
• DeepBundle is able to segment bundles that have only a few hundreds of streamlines, such as the fornix.
• DeepBundle obtains better Dice scores than RecoBunbles.

Conclusions

Their results suggest that the geometric features extracted from each fiber tract can be used to effectively parcellate the fiber tracts.

DeepBundle achieves higher Dice scores compared to RecoBundles.

DeepBundle is capable of effectively parcellating small tract bundles.

Remarks

Authors use a separate network for each bundle.

Results from only a subset of bundles (12 out of 72) are reported.

References