Embedded hyper-parameter tuning by Simulated Annealing
Introduction
In this paper, the authors present a way for combining SGD with simulated annealing (SA). The benefit of SA is to allow the optimization procedure to get out of a local minima by momentarily allowing a loss increase.
Simulated annealing
The paper is well written and easy to follow. At first, the authors report the vanilla SA algorithm:

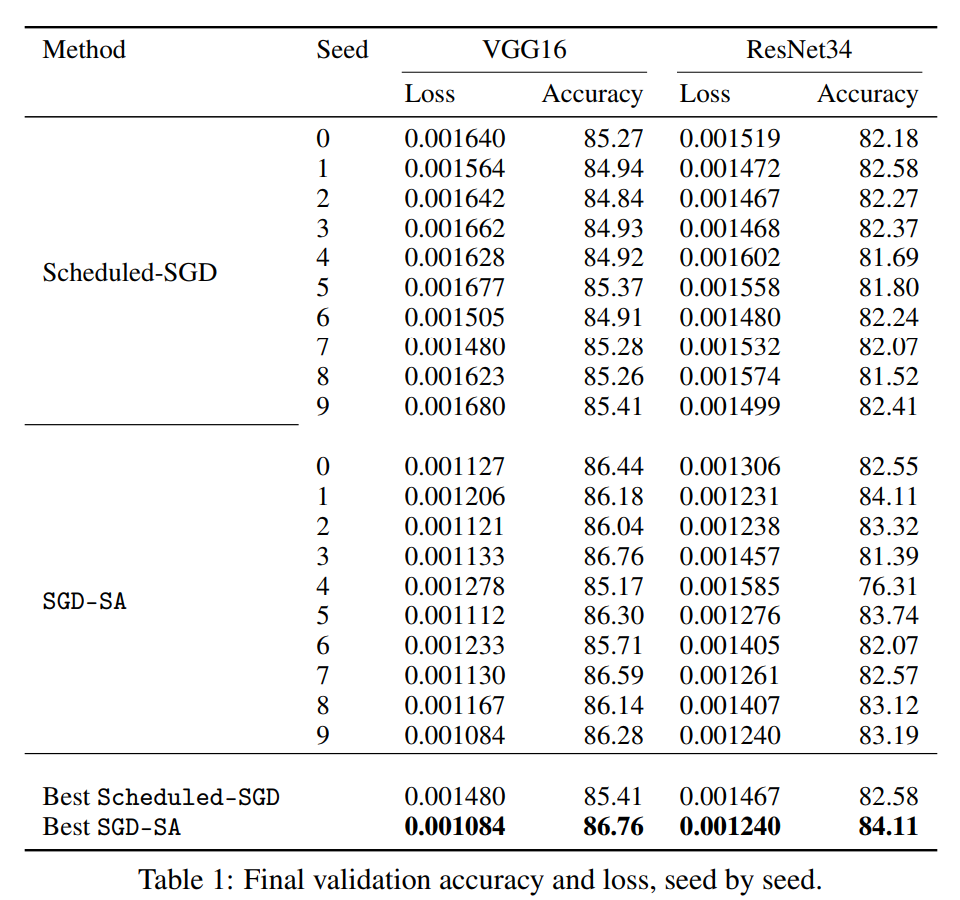
Where \(f(.)\) is a loss function and \(T\) the temperature. At the beginning, \(T\) is large thus allowing some random search. But at \(T\) decreases, only good steps corresponding to a loss decrease are allowed. In Figure 1, they show how it performs on MNIST and VGG16. The SA validation loss gets very close to that of SGD although the accuracy is not as good. But recall that this SA optimization method implies no gradient calculation!
SGD-SA
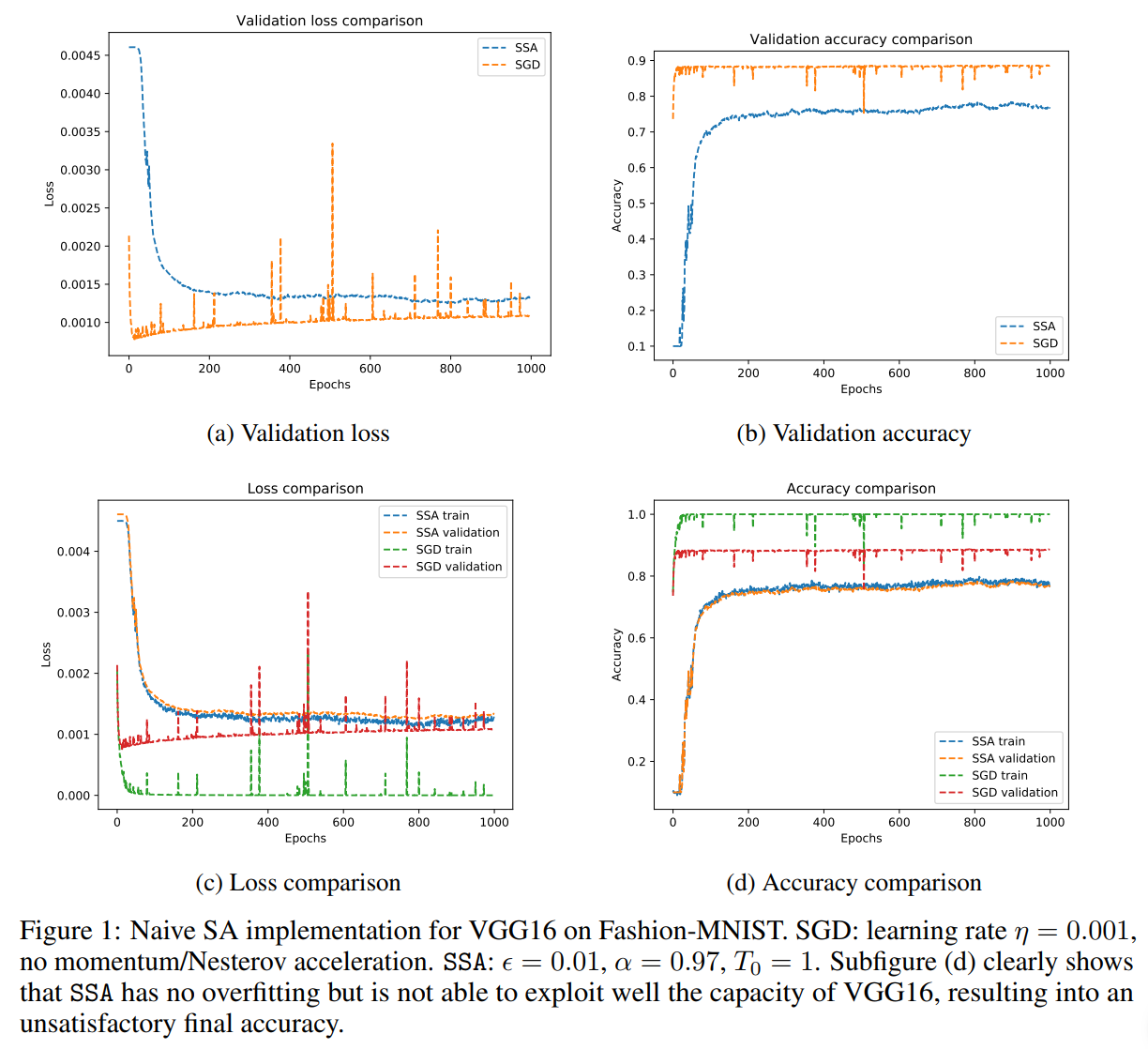
Their proposed algorithm is a mixture between SGD and SA as it randomizes the leanring rate as well as the decision to take a step in direction of the steapest descent.

They also show that at the first epochs the worsening moves are systematically accepted as opposed to later epochs. While the training accuracy curves shows a slower convergence rate of SGD-SA, it nonetheless converges towards the same accuracy than SGD.
Results
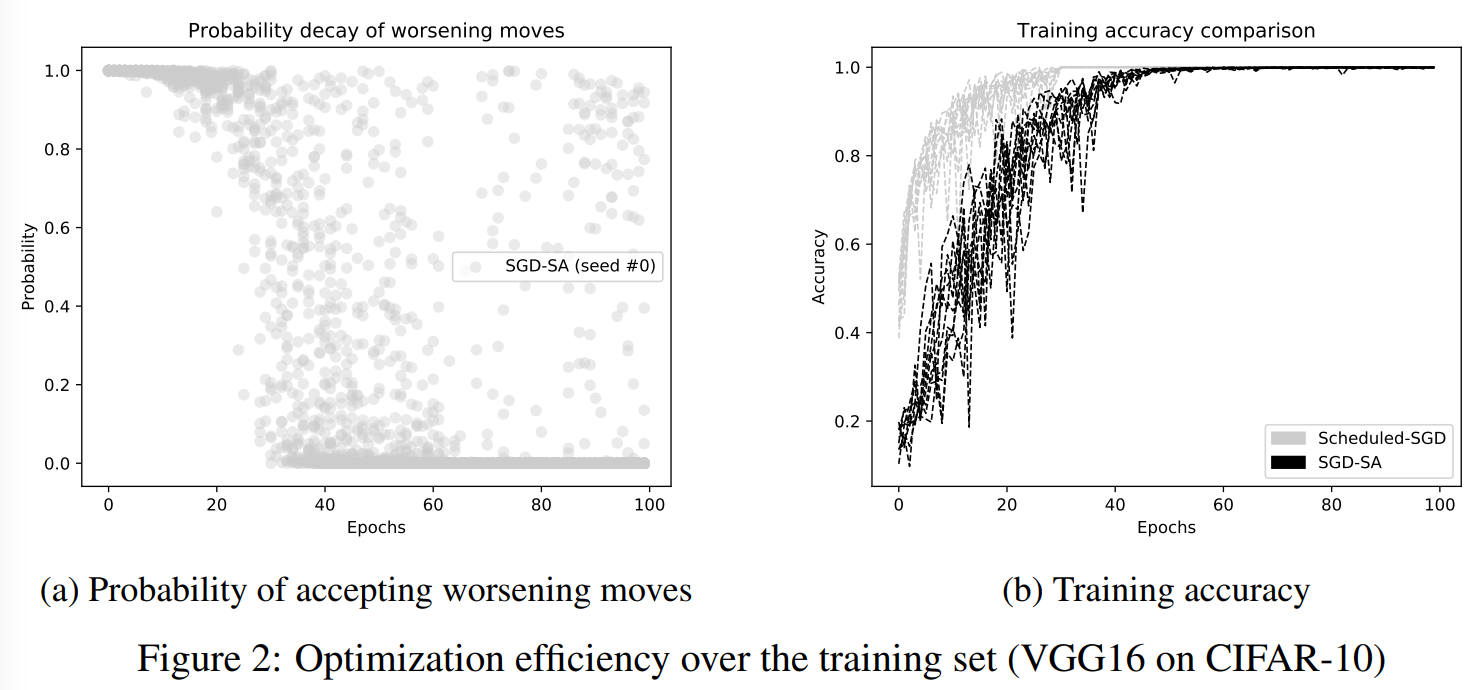
The average validation loss and accuracy obtained after several rounds of optimization on CIFAR-10 suggest that SGD-SA is better than SGD. Unfortunately, the authors provide no results for other (and more complex) classification problems as well as other optimization methods.