Highlights

The authors propose a way to bootstrap Actor-Critic (AC) Reinforcement Learning (RL) algorithms from expert demonstrations by taking DDPG as an example.

Introduction

AC-style RL algorithms work by having an actor \(\pi\) act in the environment and a critic \(Q\) output how well the actor is doing. What the critic is actually outputting is the value function \(V^\pi(s_t) = E_{a_t,s_{t+1},..}[\sum_{\tau=0}^{\infty}\gamma^\tau r(s_{t+\tau})]\) which is the discounted reward at \(s_t\). Let \(\eta(\pi) = E_{s_0,a_0,..}[\sum_{t=0}^{\infty}\gamma^\tau r(s_{t})]\) be the expected sum of discounted reward for a specific policy and \(A^\pi(s_t, a_t) = Q^\pi(s_t, a_t) - V^\pi(s_t)\) be the advantage function, telling you how good the reward from your action is compared to the expected reward at the current state.

Methods

Let’s say we have an expert policy \(\pi^*\) that performs better than our policy, which we can define with

\[\eta(\pi^*) \geq \eta(\pi)\]

which we will call constraint \((1)\)

The authors then introduce the following theorem and “prove it”:

which gives the constraint \((3)\)

\[E_{s_0^*,a_0^*,..~\pi} [\sum_{t=0}^{\infty}\gamma^t A^\pi (s_t^*,a_t^*)] \geq 0\]

which basically says that the expert always acts better or as good as expected.

The authors then give the following gradients

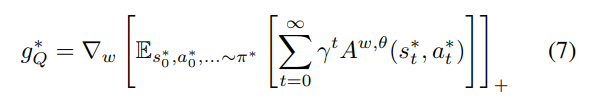
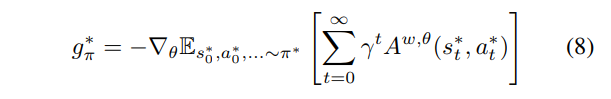
where \(w, \theta\) are the parameters for the critic and actor networks. We can then combine them to the standard DDPG gradients

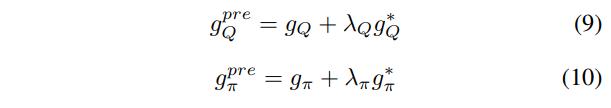
TLDR: Calculate the advantage of the expert policy. Multiply the advantage to the gradients of the weights of the critic. Add it to the gradient from the raw algorithm.

Data

The authors tested their method on the HalfCheetah, Hopper, and Walker2d OpenAI Gym environments.

Results

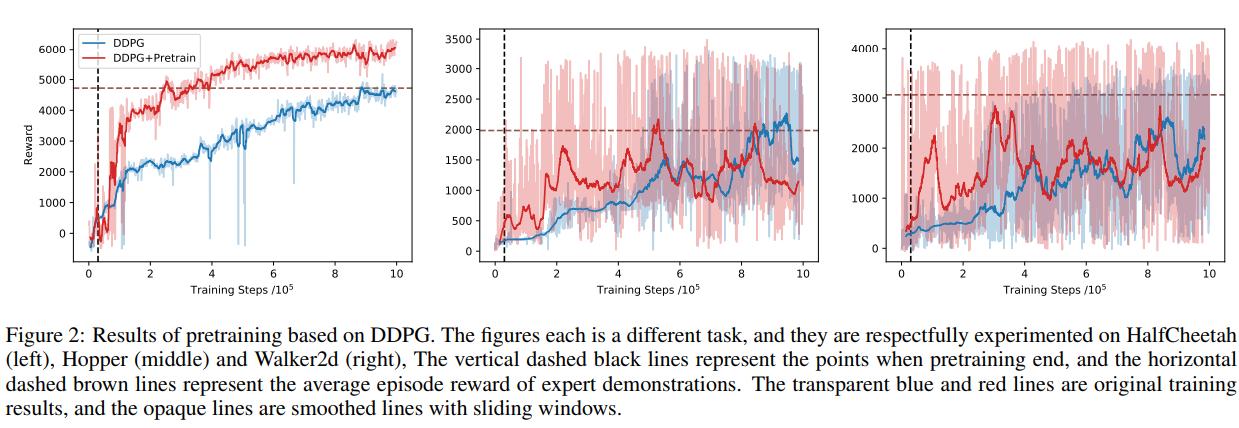
Conclusions

Pretraining Actor-Critic algorithms with expert demonstrations seem to improve performance from cold-started algorithms.

Remarks

In fact, it doesn’t really seem to improve that much in the long run, the “theorem” is quite sketchy and I’m not sure I really follow their math.