[sketchRNN] A Neural Representation of Sketch Drawings
Introduction
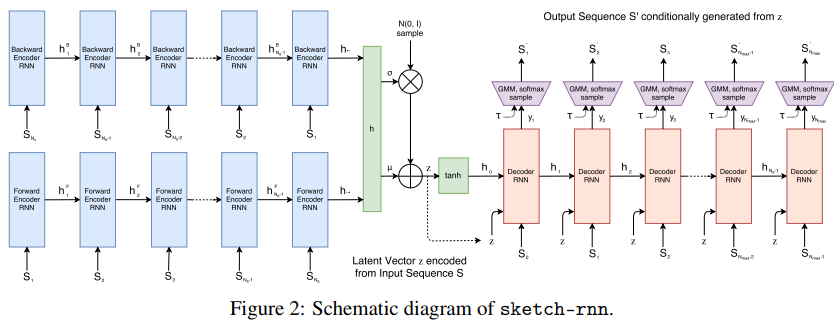
In this paper, the authors present a conditional VAE capable of encoding and decoding manual sketches. The goal is to teach a machine to draw a sketch like a human would do.
A sketch is a list of points, and each point is a vector consisting of 5 elements: \(S_i=(\Delta x, \Delta y, p_1, p_2, p_3)\) where \((\Delta x, \Delta y)\) is the offset wrt the previous point and \((p_1, p_2, p_3)\) are binary variables encoding the pen status (down, up, EndOfSketch).
Proposed method
The method is illustrated in the top figure. The encoder is a bidirectional RNN which generates a latent point, iid of a Gaussian distribution. The decoder is an RNN whose input is both the previous point \(S_i\) and the latent vector \(Z\) and the output is a GMM for \((\Delta x, \Delta y)\)
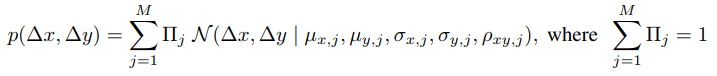
and a Softmax categorical distribution for \((p_1, p_2, p_3)\). The loss has the usual VAE shape, i.e. a reconstruction Loss plus a Kullback-Leibler Divergence Loss. The reconstruction loss has two terms namely
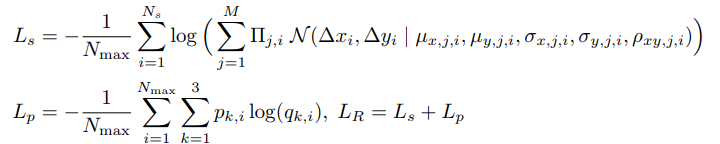
At test time, they use a “temperature” variable \(\tau\) to add more or less randomness to their method.
Results
They first show how their method works without an encoder (so only training the decoder). This leads to an unconditioned RNN generator.

They then show that their VAE can correct abnormalities.
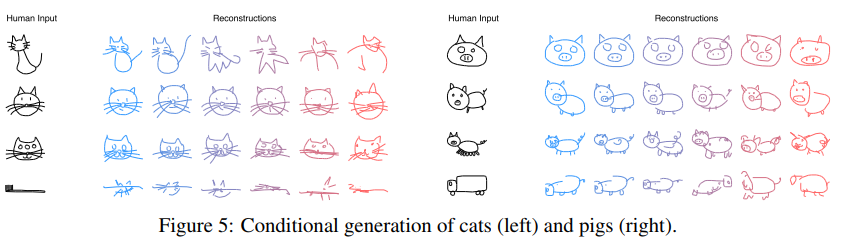
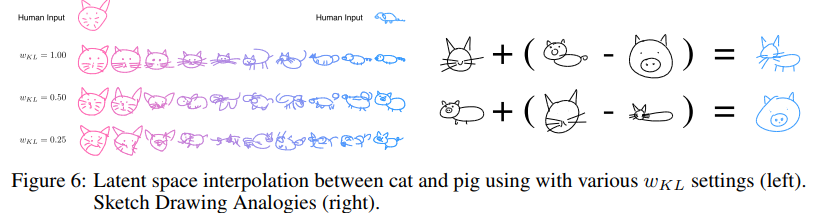
and interpolate between shapes
Even more interesting, their system can predict a sketch from an incomplete sketch.

You shall find more information on the follwing BLOG