Generative Adversarial Imitation Learning
Introduction
GAIL introduces as state-of-the-art imitation learning (IL) algorithm that leverages Generative Adversarial Networks (GANs) to match the expert’s probability distribution of state-action pairs.
Methods
Before going into the subject, let us define a couple of things:
\(\rho_\pi\), dubbed the occupancy mesure of (s,a), is the probability distribution of observing all (s,a) pairs under the policy \(\pi\). Therefore, \(\mathbb{E}_\pi[c(s,a)] = \sum_{s,a} \rho_\pi(s,a)c(s,a)\), \(c\) a cost function.
The set of valid occupancy measures can be defined as \(D \triangleq \{\rho_\pi : \pi \in \Pi\}\), \(\Pi\) the set of all possible policies. Following some complex math, it can be demonstrated that \(\pi_\rho\) is the only policy whose occupancy measure is \(\rho\)
Therefore, if we recover the expert policy’s occupancy measure, we have the same policy as the expert.
Still following some more complex maths, the two following statements are true (taken directly from the article):
IRL is a dual of an occupancy measure matching problem, and the recovered cost function is the dual optimum. Classic IRL algorithms that solve reinforcement learning repeatedly in an inner loop, such as the algorithm of Ziebart et al. [31] that runs a variant of value iteration in an inner loop, can be interpreted as a form of dual ascent, in which one repeatedly solves the primal problem (reinforcement learning) with fixed dual values (costs). Dual ascent is effective if solving the unconstrained primal is efficient, but in the case of IRL, it amounts to reinforcement learning!
The induced optimal policy is the primal optimum. The induced optimal policy is obtained by running RL after IRL, which is exactly the act of recovering the primal optimum from the dual optimum; that is, optimizing the Lagrangian with the dual variables fixed at the dual optimum values. Strong duality implies that this induced optimal policy is indeed the primal optimum, and therefore matches occupancy measures with the expert. IRL is traditionally defined as the act of finding a cost function such that the expert policy is uniquely optimal, but now, we can alternatively view IRL as a procedure that tries to induce a policy that matches the expert’s occupancy measure.
To summarize, solving the IRL problem provides a lower bound on the occupancy measure matching problem. Even better, the strong duality theorem informs us that solving the IRL problem gives us an optimal policy!
With \(H(\pi)\) the causal entropy of \(\pi\) acting as a policy regularizer, we have the following imitation learning algorithm:
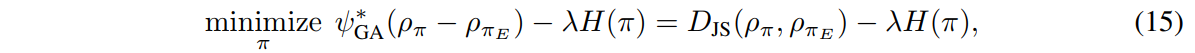
where \(\psi^*_{GA}\) corresponds to the following regularizer:
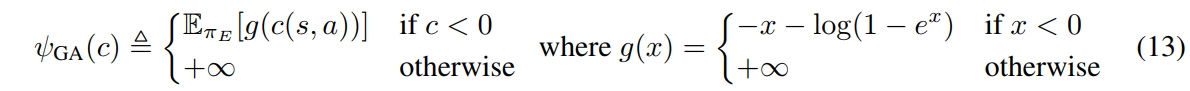
Explicitly, we wish to find a saddle point \((\pi, D)\) of the expression:
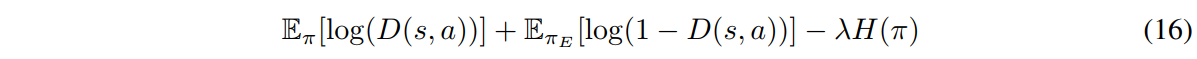
where \(D\) will discriminate state pairs that don’t come from the expert’s distribution. The Generative Adversarial Imitation Learning algorithm goes as follows:

Results
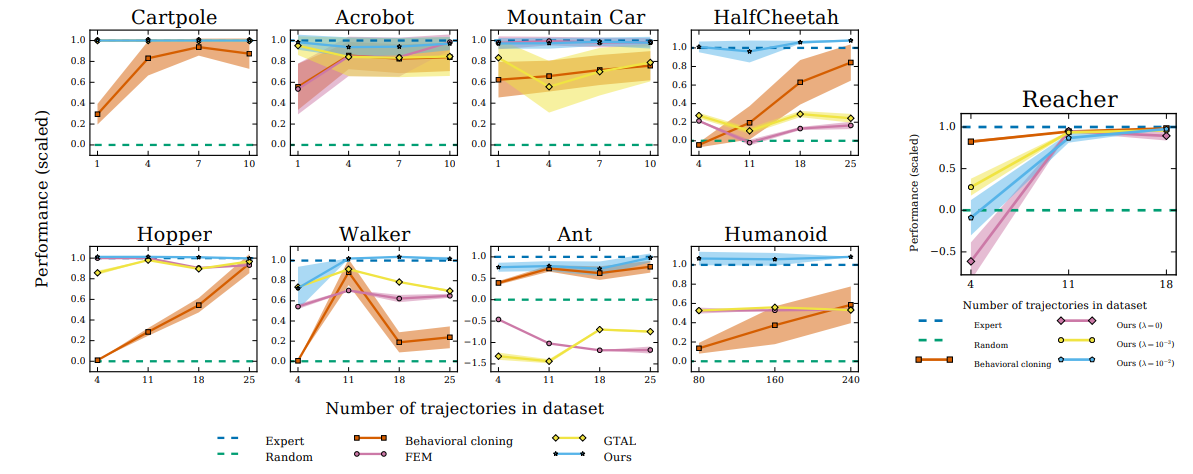
At the time of writing this post, GAIL is still considered state-of-the-art in Imitation Learning.