Introduction

PPO is currently a state-of-the-art algorithm for reinforcement learning that builds on TRPO\(^{[1]}\) and is said to have the stability of trust-region methods while being much simpler to implement, requiring only a few changes to vanilla policy gradient methods.

The paper has two main contributions: the clipped surrogate objective and multiple epochs for policy updates.

While the paper also proposes another way of constraining the policy updates to a trust region by adding a KL penalty coefficient, this latter approach is both more complicated to understand and implement and has been shown empirically to produce worse results. It will therefore not be explained here.

Clipped Surrogate Objective

Vanilla policy gradient methods work by optimizing the following loss

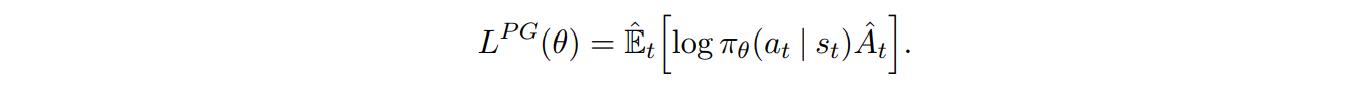
where \(\hat{A}\) is the advantage function. By performing gradient ascent on this, you will take actions that lead to higher rewards more likely. With the idea of importance sampling, we can replace the objective function with \(\hat{r_\theta}\) =

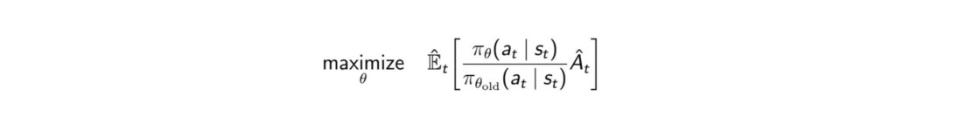
The ratio will be greater than 1 if the action \(a_t\) is more probable than it was in the old policy and between 0 and 1 if it is less probable. In TRPO, the objective function is replaced by a surrogate objective function

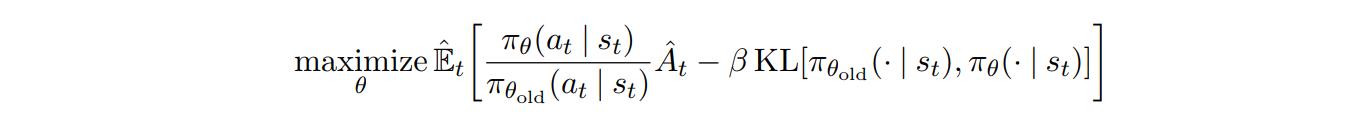
The KL term is to bound the improvement step to a trust region.

But using a KL divergence term is complicated to implement and hard to understand. Instead, the authors decided to bound the policy updated with the following Clipped Surrogate Objective function:

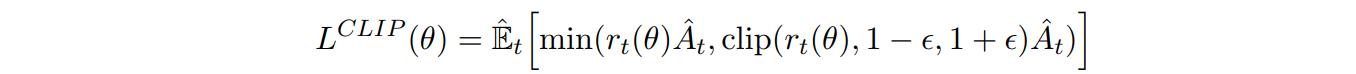
Here, \(\hat{r_\theta}\) is the previously mentioned policy ratio and epsilon is a hyperparameter (0.2 seems to work well). The clip function prevents the ratio going away from the interval \((1 - \epsilon, 1 + \epsilon)\). Taking the minimum of the clipped and unclipped objective gives a lower bound on the final objective function.

Looking at the code might make it more clear:

from any-rl

Or, more visually:

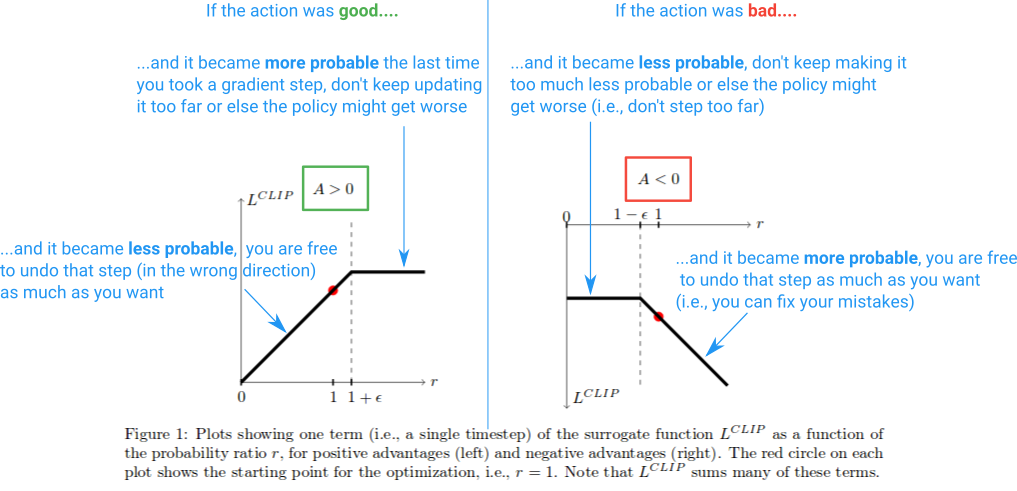from Stack Overflow

Multiple epochs for policy updates

Here is the general algorithm:

Line 6 is possible due to the clipped surrogate objective. At \(K=0\), both policies \(\pi\) and \(\pi_{old}\) are the same. As the optimization epochs go on, \(\pi\) will diverge more and more from \(\pi_{old}\) until the objective starts to be clipped and the gradient dies. Then, \(\pi_{old} \leftarrow \pi\) and a new iteration starts.

Results

The authors tested their results of a couple of OpenAI Gym environments and they achieved SOTA on almost all environments.

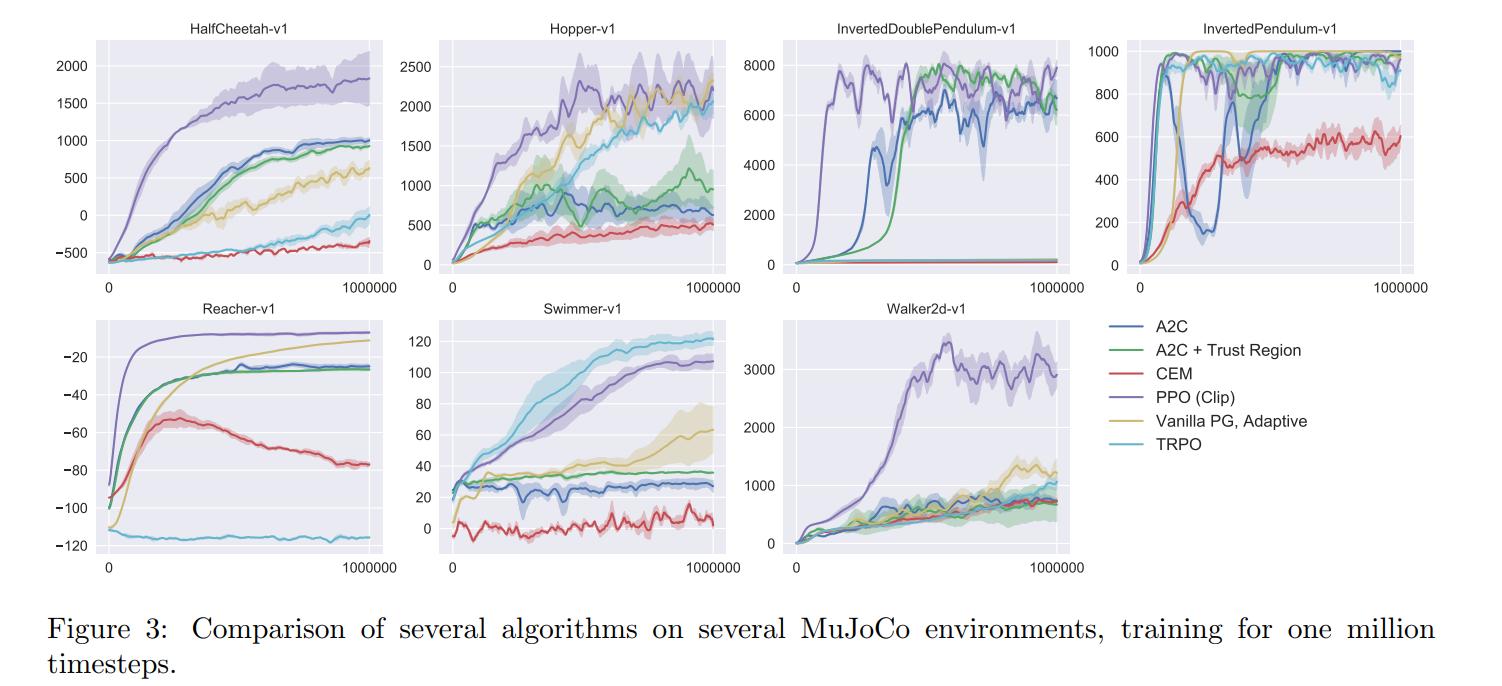
See the blog post for demonstrations

[1] : Trust Region Policy Optimization