Summary

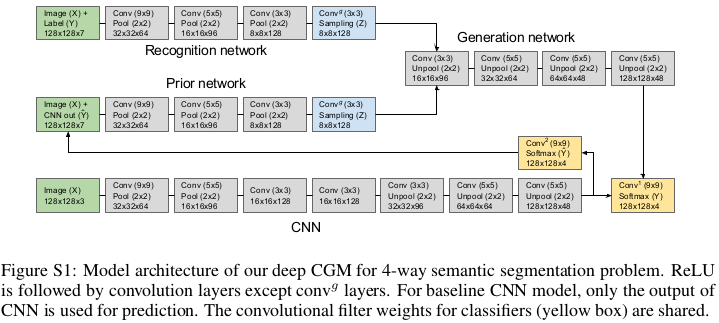
Sohn et al. propose two different (but very similar) conditional VAE which they call CVAE and Gaussian stochastic NN (GSNN). Their goal is to make structured prediction from corrupted input data. Their overall model is illustrated in the previous image.

Proposed method

The CVAE model is a modification of the VAE whose objective is the well-known variational lower bound

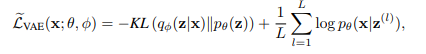
Here, \(q_\phi(z\vert x)\) is usually a neural network predicting a Gaussian distribution depending on \(x\) and \(p_{\theta}(z)\) is a prior on the latent code z, usually a zero-centered Gaussian.

For the CVAE, the aim is to generate an output \(y\) (could be an image or a segmentation as will be shown in the results section) conditioned on \(z\) and \(x\) : \(p_{\theta}(y\vert x,z)\). The objective changes to the following conditional log-likelihood:

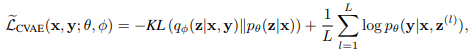
where \(z^l=g_{\phi}(x,y,\epsilon), \epsilon \sim N(0,1)\)

Overall, the CVAE consists of three networks : the recongition network \(q_{\psi}(z\vert x,y)\), the prior network \(p_\theta(z\vert x)\) and the generation network \(p_\theta(y\vert x,z)\). Interestingly, their implementation can be seen as a recurrent model.

The authors mention the existence of a gap between training and testing of the CVAE. Specifically, at testing time, \(z\) is drawn from the prior \(p_\theta(z\vert x)\), but at training time, the recognition network \(q_{\psi}(z\vert x,y)\) is used. To make prediction during training and testing the same, they set \(q_\psi(z\vert x,y)=q\theta (z\vert x)\). This resulted into the following objective

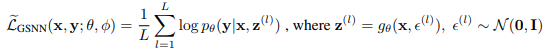
This model is called GSNN. Finally, the objectives of both models are combined in a weighted sum.

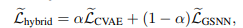
Results

Segmentation results on corrupted input data are quite convincing.