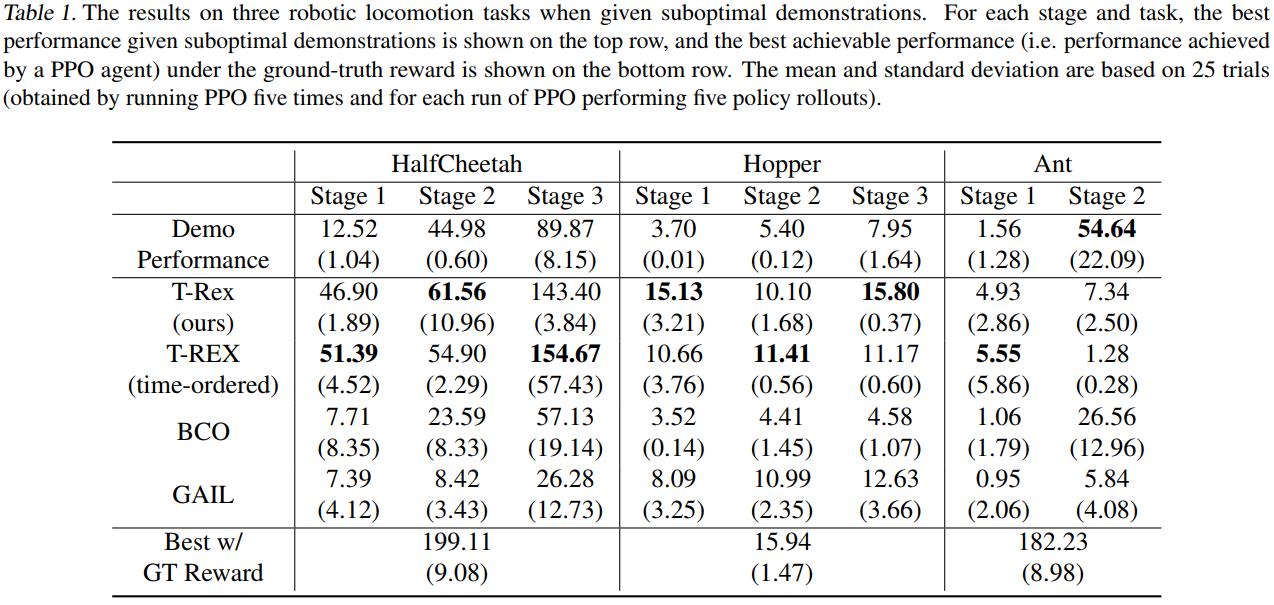
Extrapolating Beyond Suboptimal Demonstrations via Inverse Reinforcement Learning from Observations
Introduction
Inverse-Reinforcement Learning methods are usually bounded by the expertise of the demonstrator as they presume the demonstrator is optimal. The authors propose a way to circumvent this limitation by training a neural network how to tell which demonstrations are better than others. This allows the learned reward to extrapolate beyond the demonstrations and become better than the demonstrators.
Methods
The article follows closely [1] where demonstrations are “ranked” by human “jugdes”.
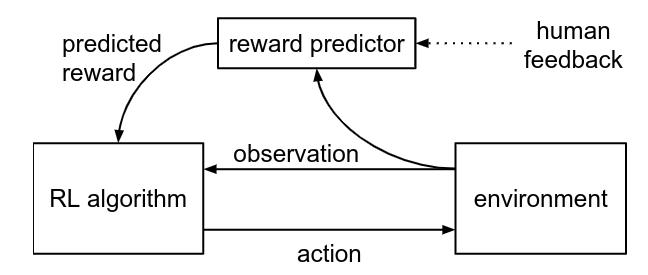
where the reward predictor is a neural network. A trajectory \(\sigma^1\) is prefered over trajectory \(\sigma^2\) if
\[(o^{1}_{0}, o^{1}_{1}, ..., o^{1}_{t}) \succ (o^{2}_{0}, o^{2}_{1}, ..., o^{2}_{t}) \rightarrow r(o^{1}_{0}) + ... + r(o^{1}_{t}) > r(o^{2}_{0}) + ... + r(o^{2}_{t})\]where \(o\) is an observation. The reward network \(\hat{r}\) is then trained with the following cross-entropy-style loss:
\[\mathcal{L(\hat{r}} = \sum_{(\sigma^1, \sigma^2, \mu) \in \mathcal{D}} \mu log \hat{P} [\sigma^1 \succ \sigma^2] + (1-\mu) log \hat{P} [sigma^2 \succ sigma^1]\]where
\[\hat{P} [\sigma^1 \succ \sigma^2] = \dfrac{exp\sum{}\hat{r}(o^1_t)}{exp\sum{}\hat{r}(o^1_t) + exp\sum{}\hat{r}(o^2_t)}\]The main difference between [1] and this article is that instead of asking humans to rate the generated trajectories, the authors assumed that a model trained to mimic a not-necessarily-optimal expert would get better over time and therefore produce increasingly better trajectories itself.
Experiments
The RL algorithm used was PPO, and to generate demonstrations, they trained agents using PPO and the ground truth reward and kept the trajectories at three different “stages”