Introduction

Conventional neural architecture search (NAS) emerged as a promising direction for jointly searching wiring patterns and which operations to perform relying generally on “Network Generators”.

The authors propose a probabilistic approch to the “network generators” which they call “Stochastic Network Generators”.

Methodology

They define a stochastic network generator as a mapping from parameter space θ to a space of neural network architectures. The parameters can contain diverse information, for example in a ResNet generator, θ can specify the number of stages, number of residual blocks for each stage, depth/width/filtersizes, activation types, etc. They also introduce a seed parameter which can be used to contstruct a random family of networks for the same parameter θ. The authors use an LSTM to sample a graph construction action (e.g., insert an operator, connect two nodes…) with hand-designed rules defined to map the sampled actions to a computational DAG.

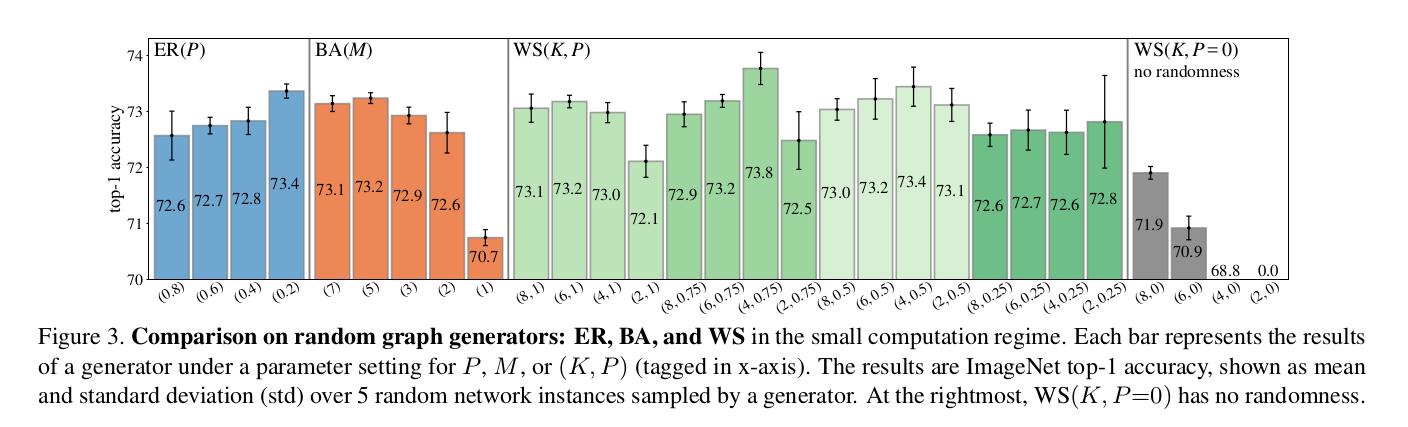
Random Graph Models

They use three method to generate graphs:

  • Erdos-Renyi (ER) : with N nodes,an edge between two nodes is connected with probability P, independent of all other nodes and edges. This process is iterated for all pairs of nodes.
  • Barabasi-Albert (BA): generates a random graph by sequentially adding new nodes with M new edges, for a node to be added, it will be connected to an existing node with probability proportional to it’s degree.
  • Watts-Strogatz (WS): N nodes are regularly placed in a ring and each node is connected to its K/2 neighbors on both sides (K is an even number). Then, in a clockwise loop, for every node v, the edge that connects v to its clockwise i-th next node is rewired with probability P. “Rewiring” is defined as uniformly choosing a random node that is not v and that is not a duplicate edge.

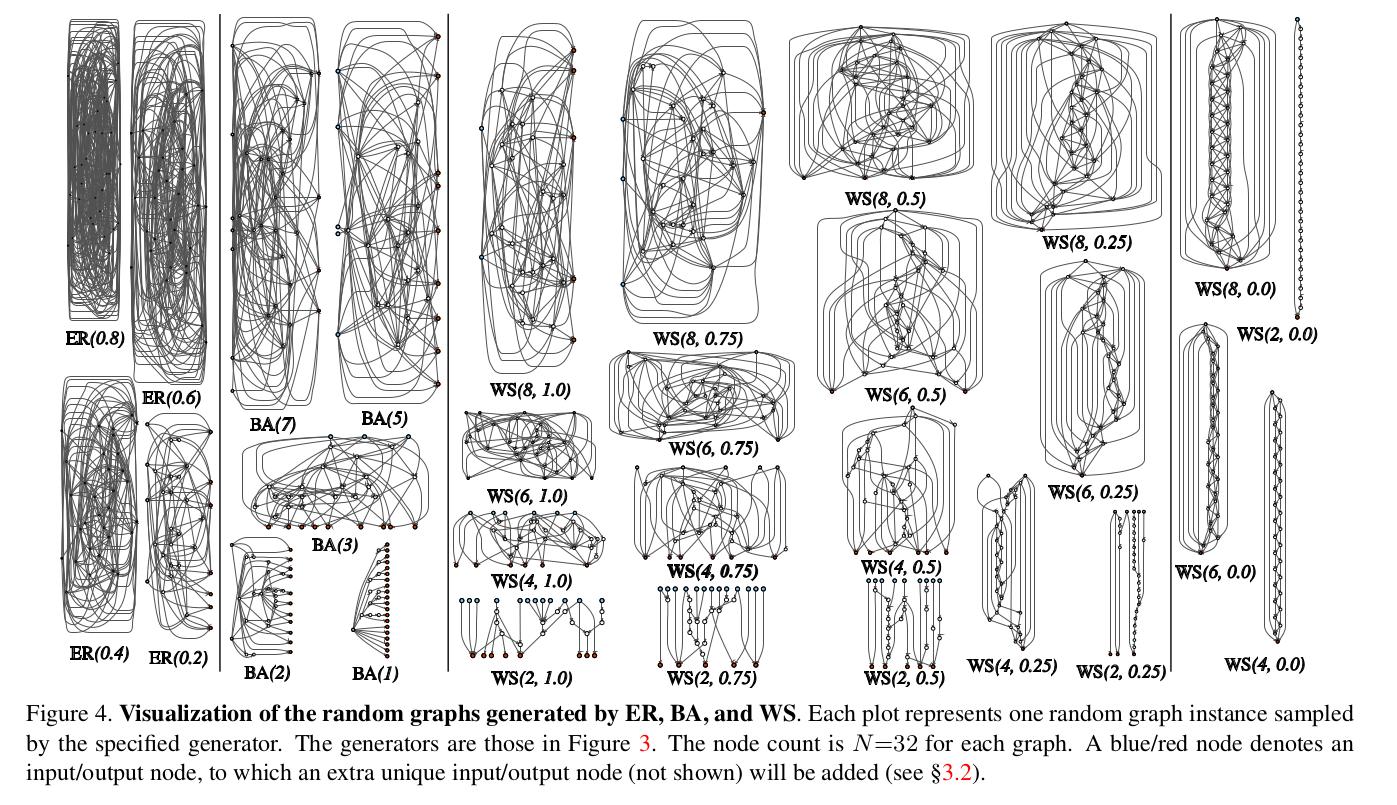
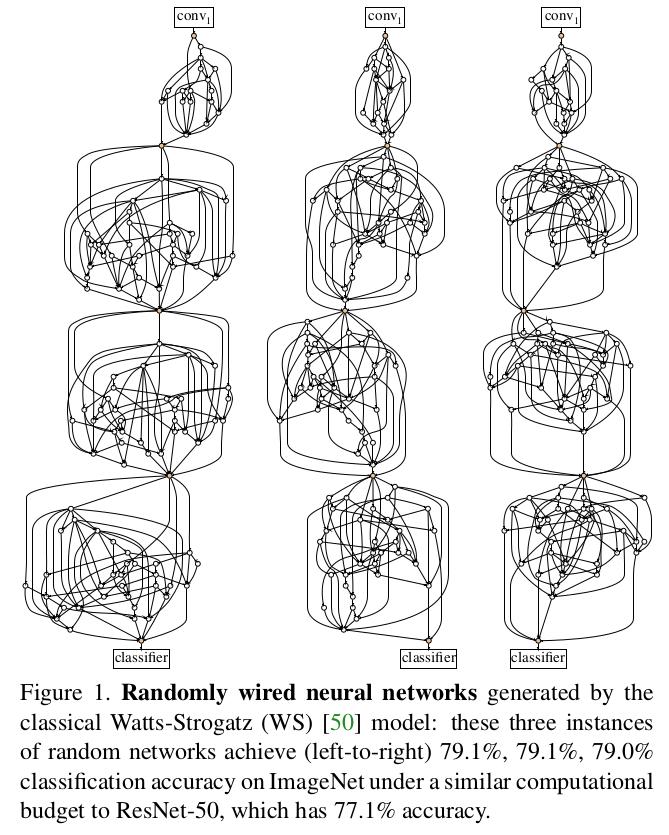
The three classical models all generate undirected graphs; they use a simple heuristic to turn them into DAGs, they assign indices to all nodes in a graph, and set the direction of every edge as pointing from the smaller-index node to the larger-index one.

Results

References

Code