Reverse Curriculum Generation for Reinforcement Learning
Highlights
- Authors propose a “reverse curriculum” method to learn the optimal policy to solve tasks through Reinforcement Learning: training is started in near-to-end states, and in subsequent iterations learning is started in states increasingly far from the goal.
- The “curriculum” is automatically generated.
- The approach solves tasks not solvable by state-of-the-art methods.
Introduction
Generally, complex task learning presents a challenge for Reinforcement Learning (RL) algorithms, either because their natural reward function is sparse and prohibitive amounts of exploration are required, or because the reward function is simply difficult to model.
Past approaches tackle these problems by exploiting expert demonstrations o by manually designing a task-specific reward shaping function to guide the learning agent.
The paper’ underpinning assumption is that a strong learning signal is obtained when training on start states that are closer to the goal. Learning from these states is also hypothesized to be fast.
Authors propose to learn these tasks without requiring any prior knowledge other than obtaining a single state in which the task is achieved. The agent is trained reversely, i.e. starting from states close to the goal and advancing increasingly towards states far from the goal.
Methods
At every policy gradient training iteration, \(N\) trajectories from some start positions \({s^i_0}_{i = 1..N}\) are collected. A number of trajectories starting from there are collected, and the success probability of the policy from those starts \(R_{\theta}(s^i_0)\) is computed. If, for a given start position \(s^i_0\), the estimated reward is not within the fixed bounds \(R_{min}\) and \(R_{max}\), the start is discarded so that it is not trained on it during the next iteration.
A sampling strategy over the distribution states that varies over the course of training is used to generate the automatic curriculum.
A different start-state distribution is used at every training iteration, but learning progress is still evaluated based on the original distribution.
State proximity is defined in terms of how likely it is to reach one state from the other by taking actions in the Markov Decision Process (MDP).
Results
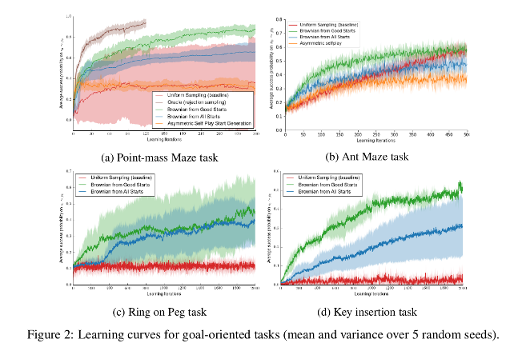
The method is tested on four environments:
- Point-mass maze task
- Ant maze task
- Ring on Peg task
- Key insertion task
Their baseline is the unfiltered start space.
Conclusions
Authors propose a method to automatically adapt the start state distribution on which an agent is trained, such that the performance on the original problem is efficiently optimized.
An agent trained in this way would be much more robust than an agent that is trained from just a single start state.
References
BAIR Berkeley log: https://bair.berkeley.edu/blog/2017/12/20/reverse-curriculum/