Spherical Harmonic Residual Network for Diffusion Signal Harmonization

Summary

Goal: Harmonize the dMRI signal differences between scanners

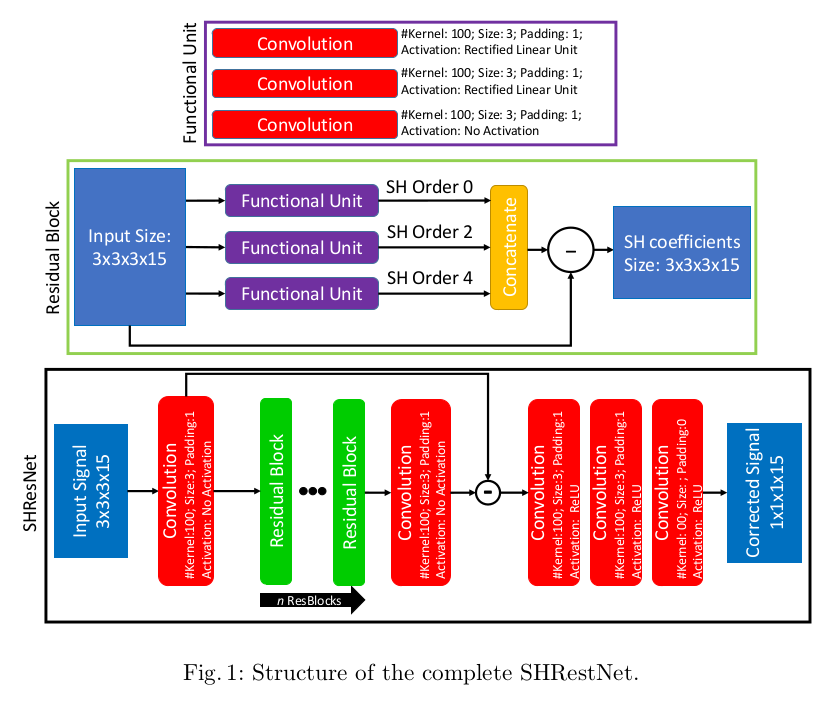
Method: Use a ResNet on 3x3x3 patches to harmonize SH coefficients voxel-wise, by learning a mapping between sites.

Highlights:

• No need for registration (at test time)
• Model-free (spherical harmonics do not impose a model on the data)

Model

• RISH projection: At test time, RISH features are used to project the harmonized signal and correct for changes in fiber orientation

where \(S_i'\) are the hamonized SH coefficients and \(S_i\) the non-harmonized SH coefficients of order \(i\).

Reminder:

RISH: Squared L2 norm for each order of SH coefficients

Results

Datasets:

CDMRI harmonization Challenge

• 10 healthy subjects, scanned on a 3T GE Excite-HD and a 3T Siemens Prisma, with 30 directions at b=1200.

Training:

• FAST registration for training subjects
• 5 epochs using Adam with batch size 256, then SGD with batch size 128 and learning rate decay…

Experiments:

• Investigate the sensitivity of the method to the number of ResBlocks n (Table 1)
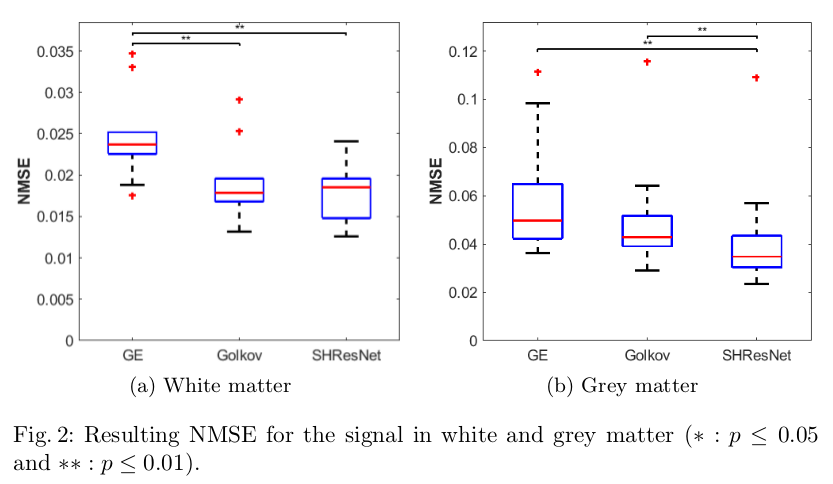
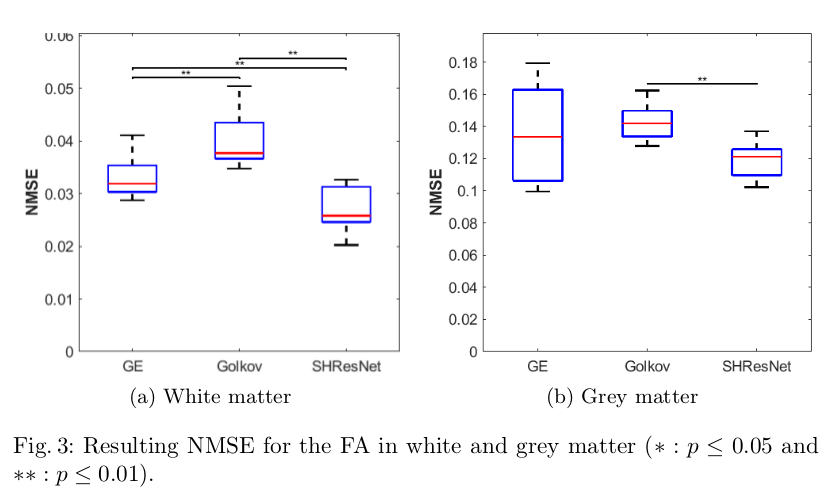
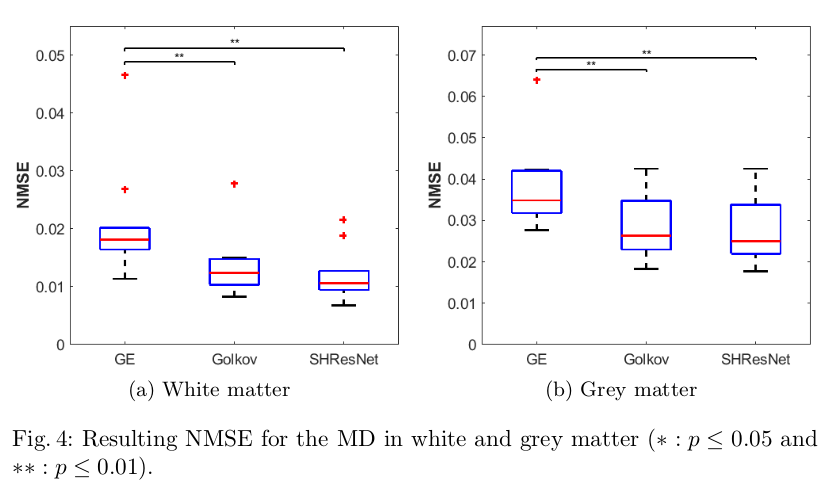
• Evaluate the ability to reduce inter-scanner variance in the signal itself and metrics like FA/MD (Figures 2,3,4)
• 10-fold cross-validation using the 10 subjects (8 training, 1 validation, 1 test).

The only reported baseline is the Golkov method¹, a 3-layer, 150 units neural network with ReLU and Dropout designed, applied on a single voxel at a time; it was “designed” for the estimation of scalar measures from diffusion data, and seems completely unrelated to harmonization.

There is no classical method baseline…