Summary

Problem : Inter-site variability in the diffusion MRI signal poses problems for tractography, segmentation, and other types of analysis.

Proposed solution : Data harmonization by mapping the SH coefficients from a target site to an arbitrarily chosen reference site.

Detailed problem

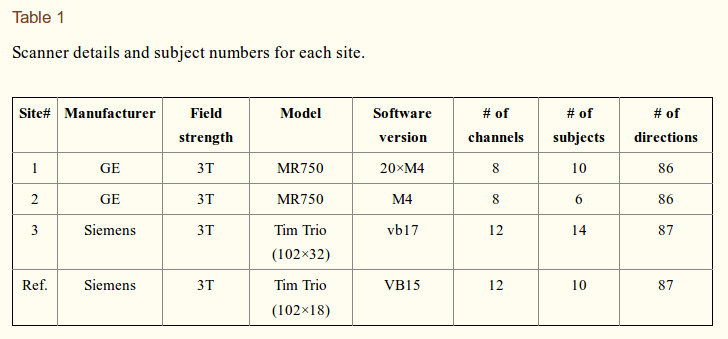
[The] inter-site variability in the measurements can come from several sources, e.g., subject physiological motion, number of head coils used for measurement (16 or 32 channel head coil), imaging gradient non-linearity as well as scanner related factors. This can cause non-linear changes in the images acquired […]. Inter-site variability in FA can be upto 5% in major white matter tracts and between 10-15% in gray matter areas. On the other hand, FA differences in diseases such as schizophrenia are often of the order of 5%.

Standard methods to address this problem :

  • perform analysis at each site, then do a meta-analysis (impossible for data-driven methods), or
  • use a statistical covariate to account for signal changes that are scanner-specific (not applicable to tractography beacause of region-specific differences).

The proposed method:

  • takes into account region-specific differences;
  • harmonizes the signal by comparing to a reference using several “Rotation-Invariant Spherical Harmonic” (RISH) features;
  • uses a region-specific linear mapping between the RISH features to remove scanner specific differences in the white matter;
  • is the first work to address the issue of dMRI data harmonization without using statistical covariates.

Figure 1 Outline of the proposed method for inter-site dMRI data harmonization

Rotation-Invariant Spherical Harmonics (RISH) features

Reminder: Spherical harmonics

\[S \approx \sum_i \sum_j C_{ij} Y_{ij}\]

The signal S is approximated as a sum of spherical functions \(Y_{ij}\) of order \(i\) and phase (or degree) \(j\), weighted by coefficients \(C_{ij}\).

The “energy” of the SH coefficients for each order is defined as the \(L_2\) norm, and forms a set of rotation invariant features:

\[||C_i||^2 = \sum_{j=1}^{2i+1} (C_{ij})^2\]

The authors define the RISH features of the target site as the expected value of the energy for orders 0,2,4 and 6, for the \(N_k\) subjects of site \(k\):

\[\mathbb{E}_k ( \left [ ||C_i||^2 \right ] ) = \frac{1}{N_k} \sum_{n=1}^{N_k} \left [ || C_i(n) ||^2 \right ]\]

Freesurfer is used to compute 8 specific anatomical brain regions :

  • frontal
  • parietal
  • temporal
  • occipital
  • brain stem
  • cerebellum
  • cingulate-corpus-callosum complex
  • centrumsemiovale-insula

In each region, the sample average RISH features \(\mathbb{E}_k (\cdot)\) are computed.

Figure 2 RISH features in the white matter for different SH orders and sites

The goal is then to find a mapping \(\Pi (\cdot)\) such that all scanner related differences are removed :

\[\mathbb{E}_k ( \Pi (||C_i||^2) ) = \mathbb{E}_r (||C_i||^2)\]

where \(r\) is the reference site and \(k\) is the target site.

Thus, the “group” mapping is given by

Equation 5:

\[\Pi ( ||C_i(n)||^2) = ||C_i(n)||^2 + \mathbb{E}_r - \mathbb{E}_k = \sum_j C_{ij}(n)^2 + \Delta \mathbb{E}\]

(Note that the mapping is specific for each SH order and for each brain region)

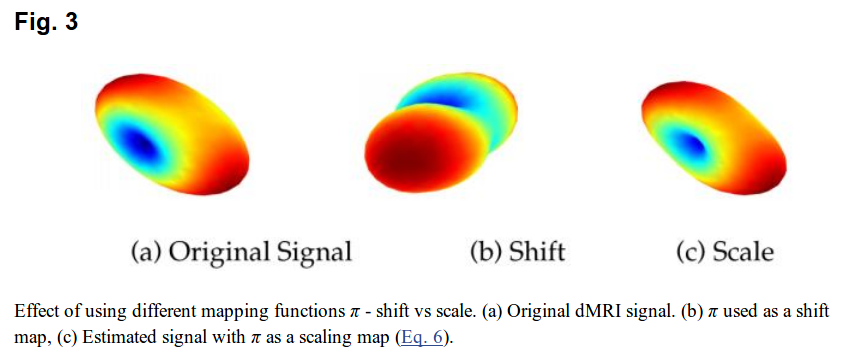
Then, all there is left to do is to change the SH coefficients in each voxel to satisfy Equation 5 for each region. There are 2 possibilities, shifting the coefficients (adding a delta) or scaling (multiplying by a delta).

  1. Shift: \(\pi(C_{ij}) = C_{ij} + \delta\)
  2. Scale:

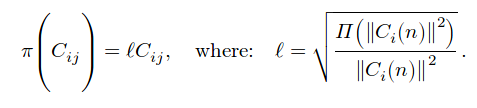
Shifting can cause coefficients to change sign, which is ill-posed for SH, as seen in figure 3.

Experiments

Tract-based spatial statistics:

Statistical test for group differences:

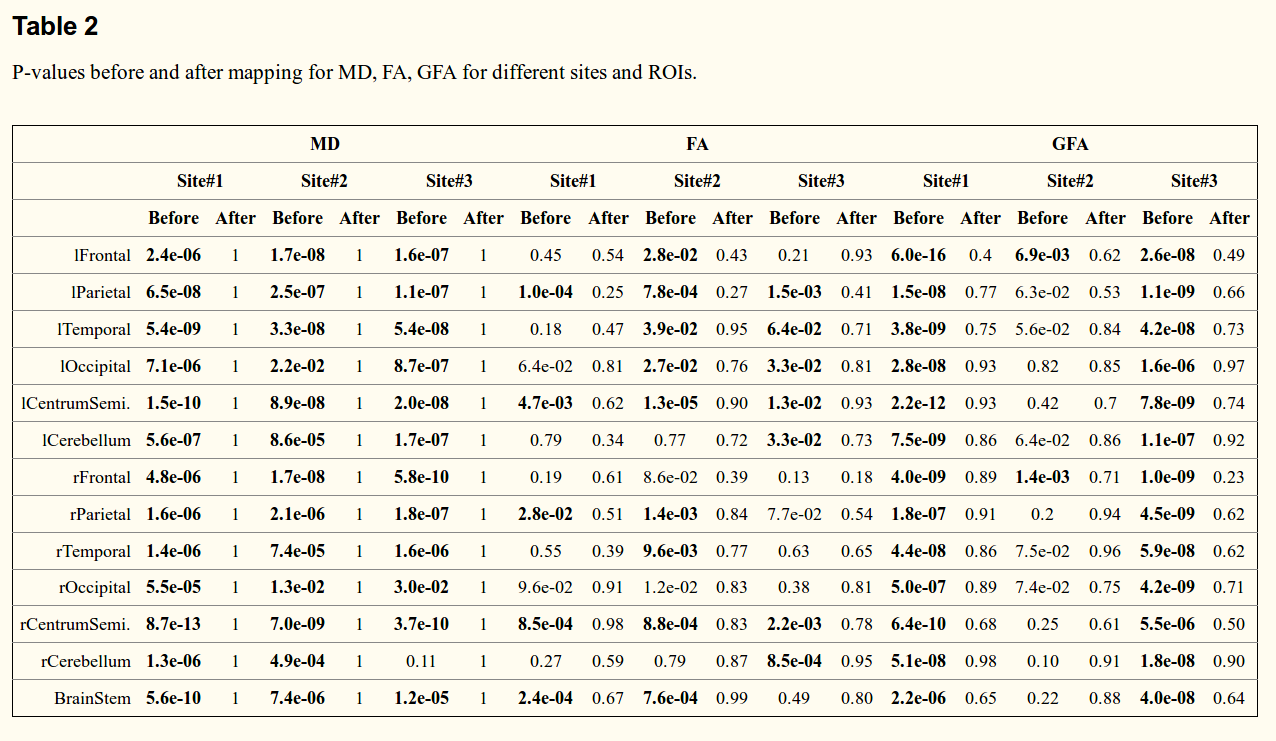
The tests show there is “no statistical difference” after harmonization.