Summary

This paper presents a method to prevent the vanishing gradient problem in LSTMs, specifically for the linear path of the cell state, which carries long term information. They show better convergence and stability in LSTMs using their proposed method.

Method

The authors show that when the LSTM weights are large in magnitude, the gradients flowing through the linear path (cell state) get suppressed.

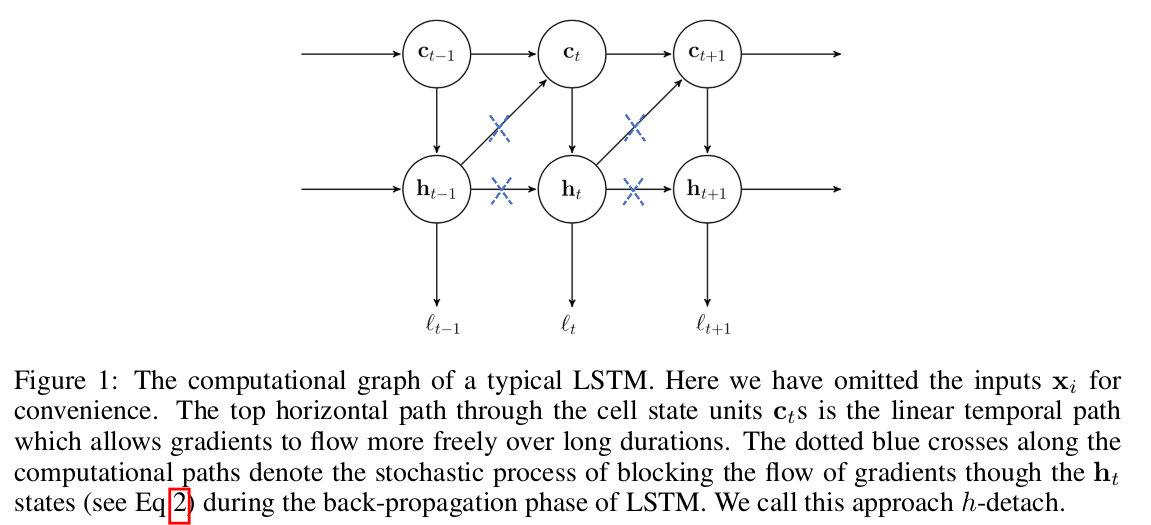
To fix the problem, they propose a stochastic algorithm that, in expectation, scales the individual gradient components. Specifically, they stochastically prevent gradient from flowing through the h-state of the LSTM.

Reminder: LSTM Equations

Skipping the mathematical details, the gradient flowing through the cell state paths is linearly bounded by the number of steps, but the gradient flowing through the other paths is unbounded and is polynomial with regards to the weight matrices. Thus, the authors propose to dampen the magnitude of the gradient coming from the other paths in order to let the cell state gradient flow, using a kind of “dropout” on the hidden state gradient.

As an aside benefit, using dropout on the gradient of the hidden state means that less computation is needed while training.

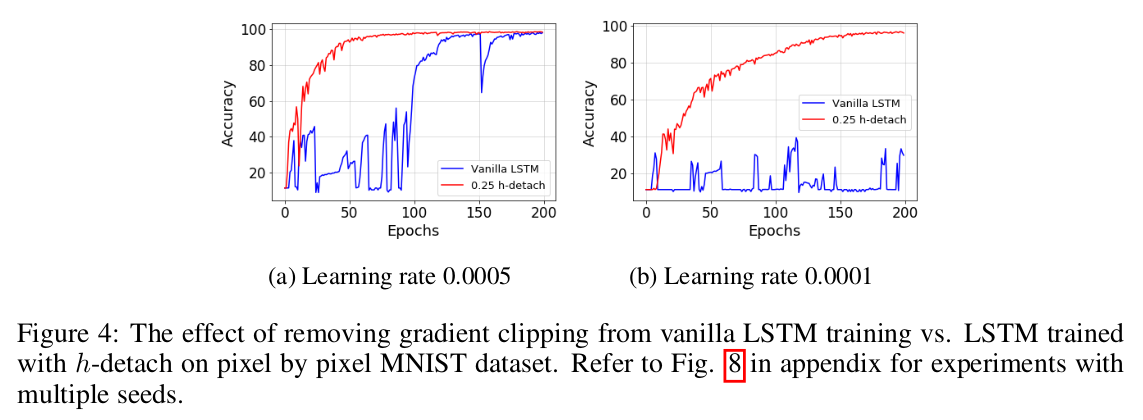
Also, while the experiments show that using h-detach allows for stable training even without gradient clipping, the authors recommend to keep gradient clipping (because the gradient magnitude depends on the detach probability p).

For stacked LSTMs, there are two possible strategies: either 1) sample one Bernoulli at each step and detach the gradient of all layers, or 2) stochastically detach each layer separately. The authors did not do any experiments for stacked LSTMs however.

They also ran experiments on language modeling tasks, but did not notice any benefit from using h-detach.

Experiments

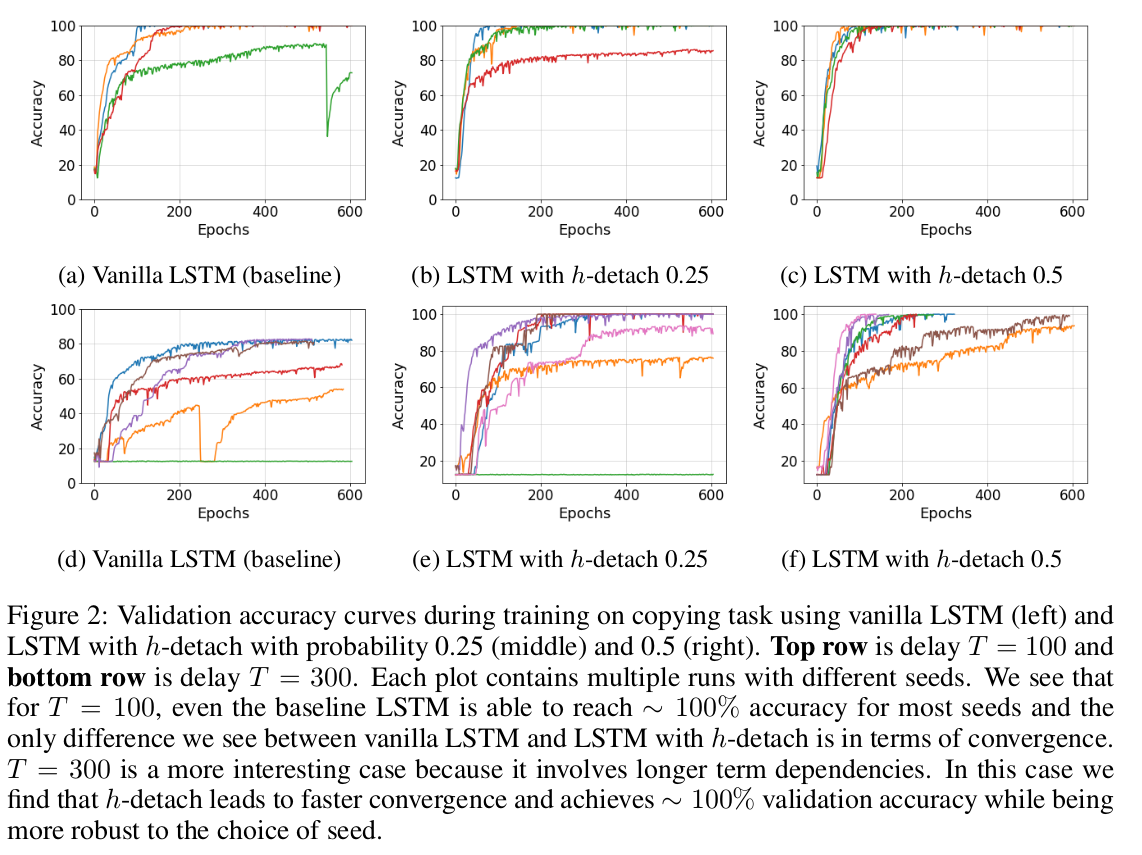
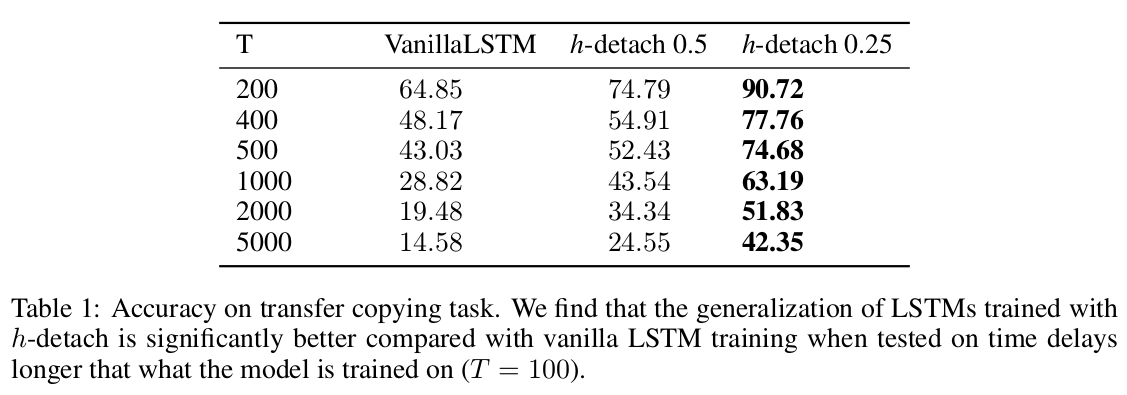
Copying task

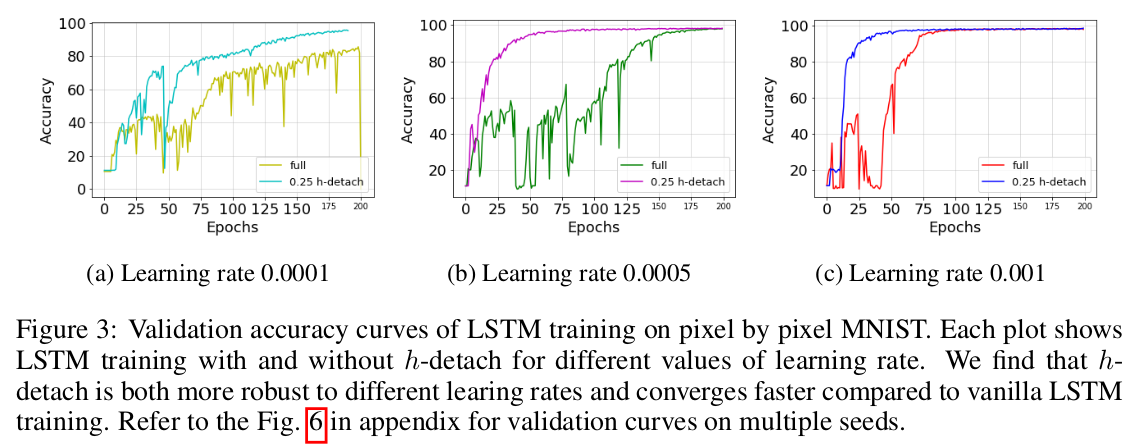
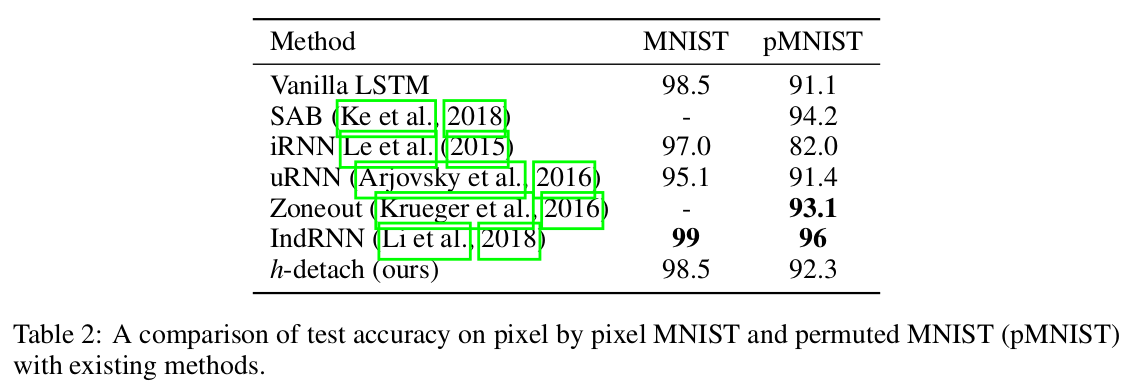
Sequential MNIST

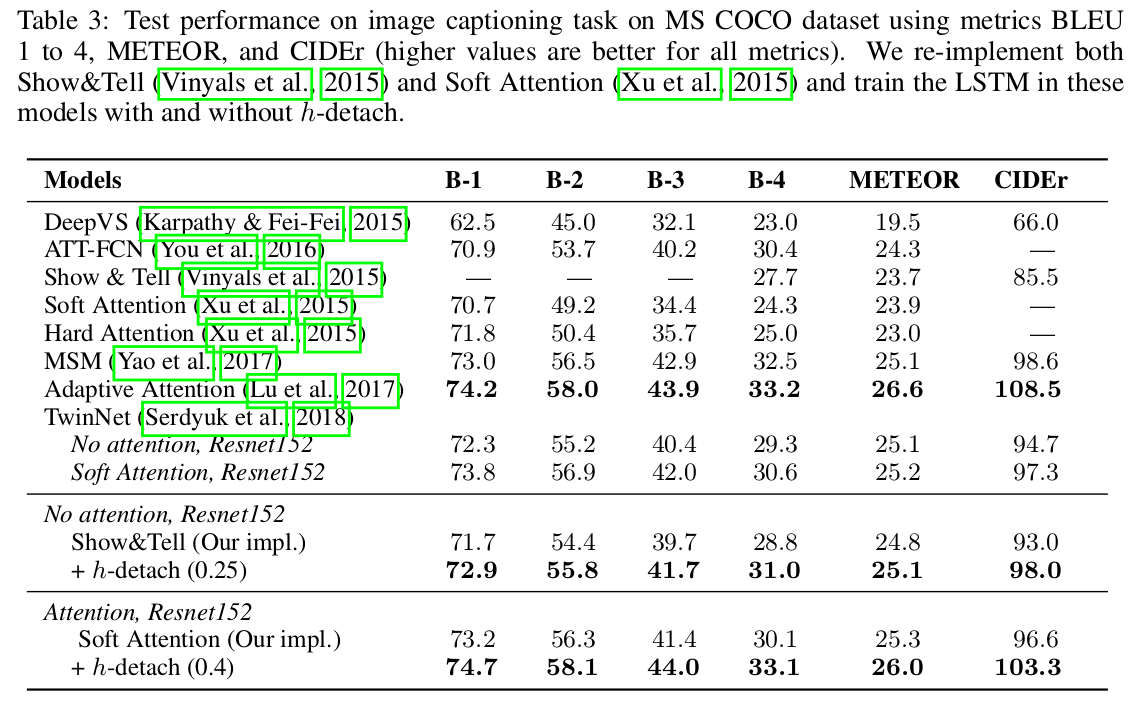
Image captioning

Ablation study