Introduction

In reinforcement learning, there are two main approaches to learn how to behave in the environment: A model-based approach where the agent tries to learn the dynamics and rewards of the environment and then uses a planning algorithm to find the best course of action, and a model-free approach, where the agent only tries to learn a policy of action to take, or tries to estimate correctly the rewards associated with the environment, which makes the decision process trivial.

In this paper, the authors try to leverage both methods in a single architecture to have better generalization, more interpretability and better transfer learning.

CRAR

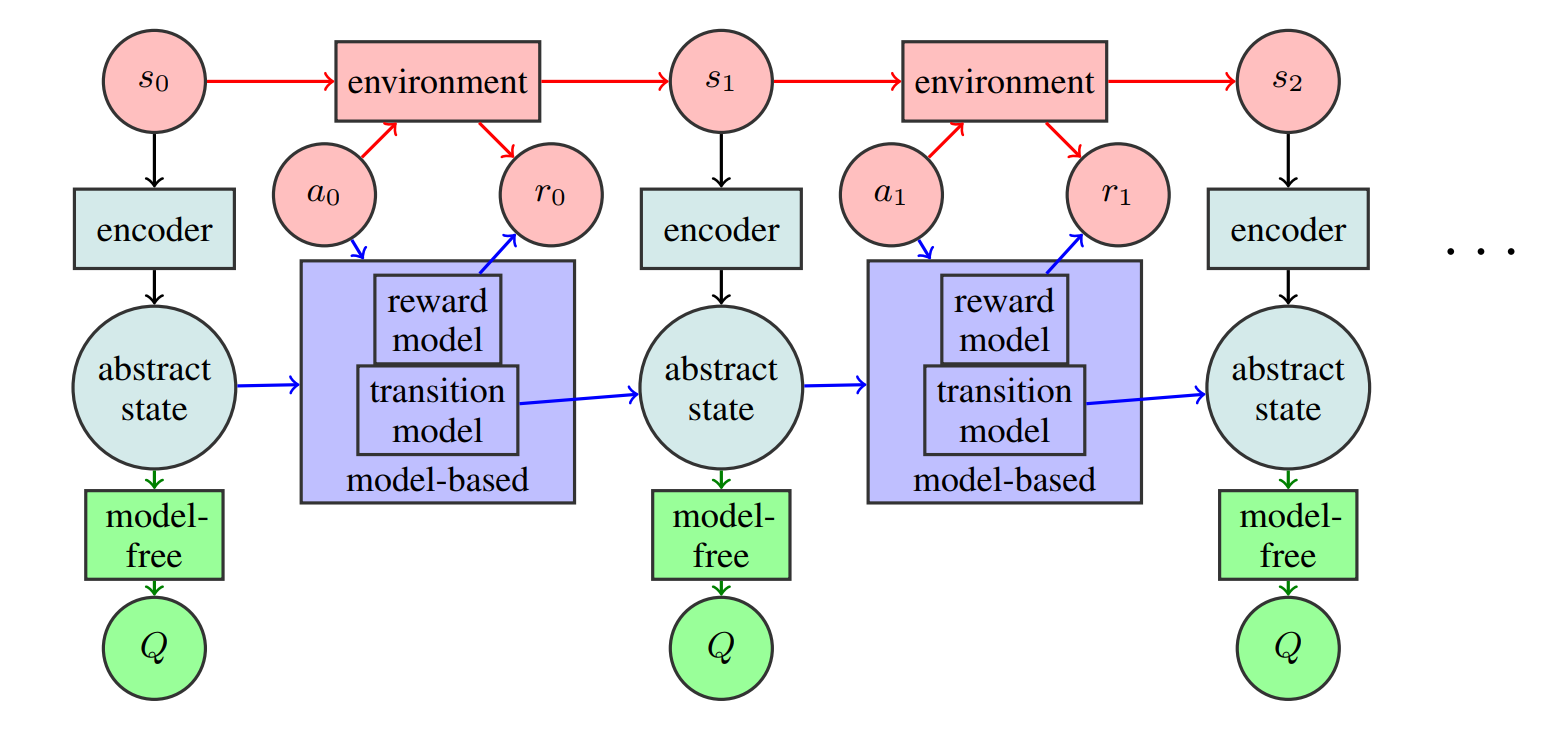
At each time step, an encoder tries to build a good simple representation of the actual state (or observation) of the environment. The model-based approach then tries to model the transition dynamics and rewards of the abstract model, and the model-free method tries to estimate the Q function associated with it.

Learning through an abstract representation instead of the actual environment has several advantages. Namely, it enables more efficient planning and simple transition dynamics within the model-based approach and allows for new exploration strategies.

Planning

Let’s define the abstract state as

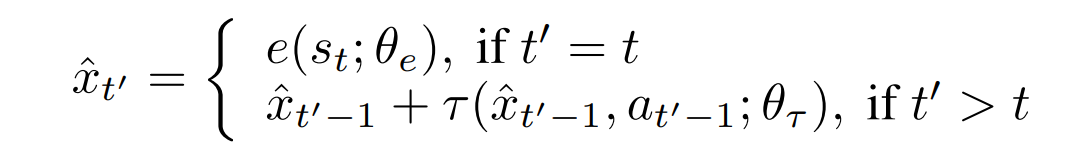
where \(e\) is the encoder, \(\tau\) the transition dynamics and \(t\) the timesteps. Planning is then done recursively as

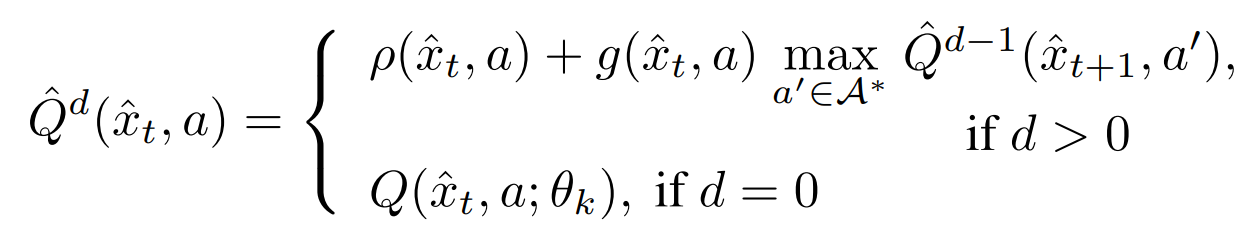
with \(\rho\) the learned reward, \(g\) the learned discount factor and \(d\) the “depth” of the planning (future time steps). The plan is then defined as

.

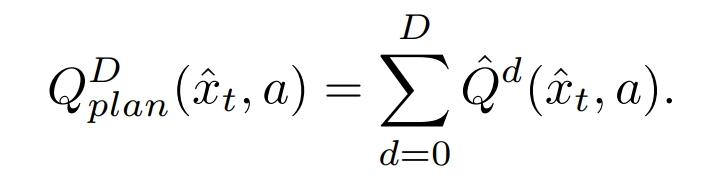Results

Interpretability

The first task considered was a labyrinth with no reward and terminal state.

The authors wanted to test the interpretability of their abstract representation

We can see above that the abstract representation provides a much more interpretable representation of its environment than T-SNE.

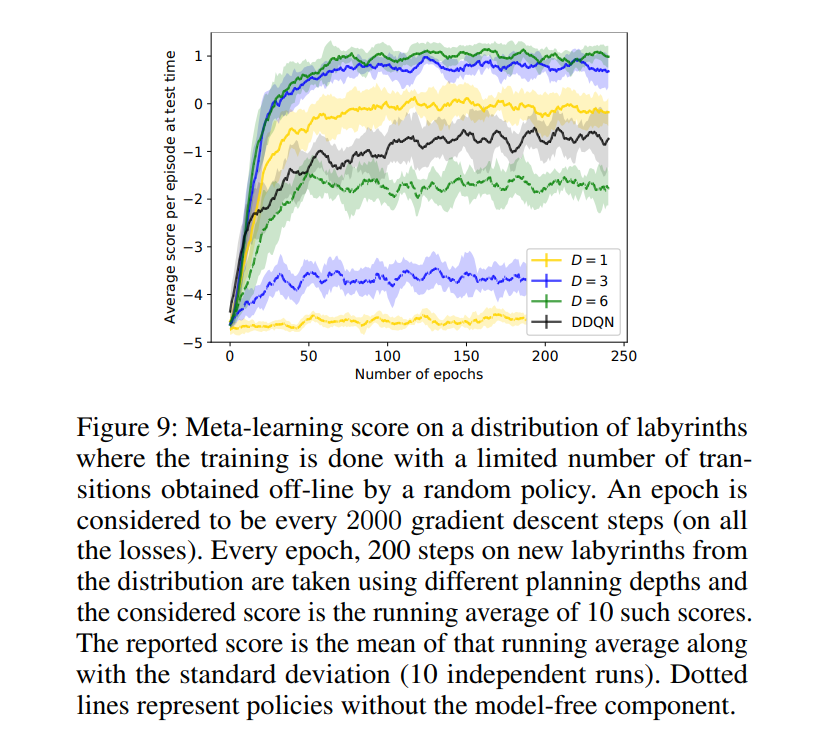
Meta-learning

The second task considered was a distribution of labyrinth, with one example below

We can then see that the architecture generalizes well on the family of a labyrinth, contrary to a simple DDQN component (the architecture without the model-based part) or the architecture without the model-free part (dotted-lines)

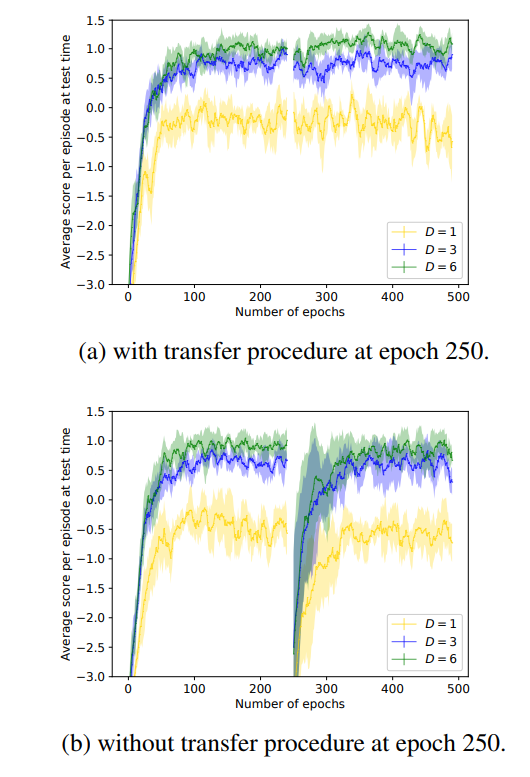
Transfer learning

Still on the same problem of labyrinths, the authors then wanted to verify if the architecture can support component swapping for transfer learning problems. To test this, they trained the algorithm on the labyrinth-distribution problem, and after some epochs, inverted the value of pixels in the images, both in the environment and states in memory. We can see with the graph below that the architecture performs as well as before the transfer procedure, while it has to re-learn without it.