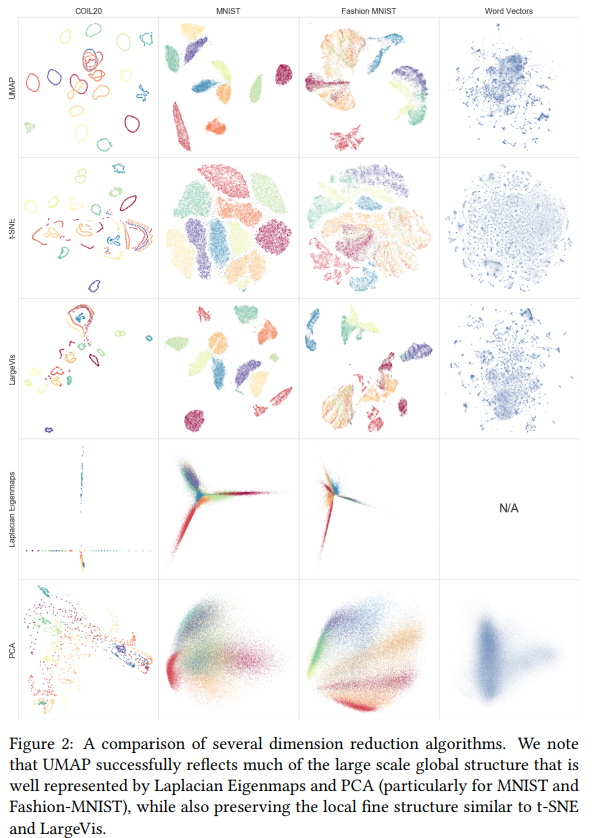
Uniform Manifold Approximation and Projection (UMAP) is a new technique for dimensionality reduction in the family of “neighbour graphs” techniques (as opposed to the “matrix factorization” family such as PCA).

The paper is quite math-heavy but here’s the TLDR:

  • Let’s assume that our dataset is distributed uniformly on a manifold and that this manifold is locally connected.
  • Let’s create a fuzzy metric that forces the “uniform” behaviour on the manifold (a Reimanian metric).
    • \(w_i(X_i, X_j) = exp(-(d(X_i, X_j) - \rho_i)/ \sigma_i)\) where d is a distance function, \(\rho_i\) is the distance to \(X_i\) nearest neighbour and \(\sigma_i\) is the diameter of the neighbourhood.
  • Since this metric is not symetrical, the actual metric is : \(f(\alpha, \beta) = \alpha + \beta - \alpha * \beta\). Where \(alpha = w_i(X_i, X_j)\) and \(beta = w_j(X_i, X_j)\).

We then create an embedding \(w'\) which will embed our data in the lower space (initialized randomly). Finally we optimize the \(w'\) using the crossentropy between \(w'\) and \(w\) using SGD.

\[C(w, w') = \sum_{i\sim j} w(i,j)log(\frac{w(i,j)}{w'(i,n)}) + (1 - w(i,j)) log(1 - \frac{w(i,j)}{1 - w'(i,n)})\]

Why is this fast?

  • Need to compute the k-NN only once.
  • The comparison is only done on the neighbours of \(X_i, X_j\).

Features:

  • Fast (it is using Numba for LLVM compilation)
  • Can be used on new data points.
  • The classes can be provided to get a better embedding while keeping the relation between classes.

  • Solid theoretical foundation (Category, Topology)

Code

Blog

Awesome Talk