Summary

This paper introduces Associative Compression Networks (ACNs), a new framework for variational autoencoding with neural networks. The system differs from existing variational autoencoders (VAEs) in that the prior distribution used to model each code is conditioned on a similar code from the dataset.

The authors remind that the VAE latent space do not provide very good high-level of abstraction of the data and that the goal of ACN is answer that problem.

Specific details

Starting from the usual ELBO VAE loss

\[L^{VAE}(x) = KL(q(z|x)||p(z)) - E_{z\sim q}[log r(x|z)]\]

the author then summarize their method as follows:

Associative compression networks (ACNs) are similar to VAEs, except the prior for each \(x\) is now conditioned on the distribution \(q(z|\hat{x})\) used to encode some neighbouring datum \(\hat{x}\). We used a unit variance, diagonal Gaussian for all encoding distributions, meaning that \(q(z|x)\) is entirely described by its mean vector \(E_{z\sim q(z|x)}[z]\), which we refer to as the code \(c\) for \(x\). Given \(c\), we randomly pick \(\tilde{c}\), the code for \(\hat{x}\), from KNN(\(x\)), the set of K nearest Euclidean neighbours to \(c\) among all the codes for the training data. We then pass \(\tilde{c}\) to the prior network to obtain the conditional prior distribution \(p(z|\tilde{c})\) and hence determine the KL cost. Adding this KL cost to the usual VAE reconstruction cost yields the ACN loss function :

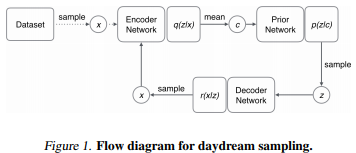
\[L^{ACN}(x) = E_{\tilde{c}\sim KNN(x)}KL(q(z|x)||p(z|\hat{c})) - E_{z\sim q}[log r(x|z)]\]

They also provide an interesting sampling procedure which they call daydream.

Experiments

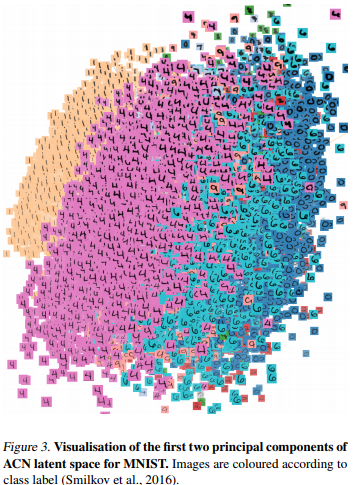
They show that the latent space recovered by ACN is more descriptive of the input data. They shown this by training a classifier on several latent space (Table 3) and showing the first two pincipal components of the ACN latent space. Daydream results are shown in Fig.9. Various information theory results are presented in the paper.