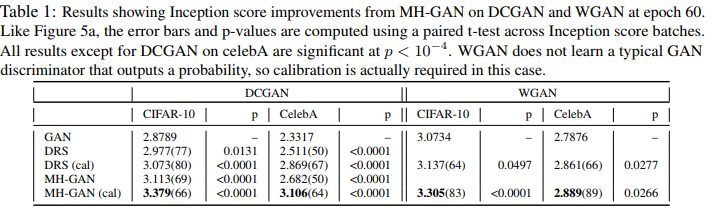
Metropolis-Hastings GAN (MH-GAN) modifies the way we do inference on the generator at test time. While common GAN architectures simple draw from the generator randomly, MH-GAN uses a Metropolis-Hastings scheme to select the best sample possible. This scheme belongs to the wide family of MCMC methods where you draw a chain of samples. A new sample \(x'\) is accepted over the current sample \(x\) with probability \(\alpha\):

\(\alpha(x', x) = min(1, \frac{D(x)^{-1} - 1}{D(x')^{-1} - 1})\) \(D(x) = \frac{p_D(x)}{p_D(x) + p_G(x)}\)

where \(p_D\) is the data density and \(p_G\) is the density of samples from G. In practice, this score is given by the discriminator.

They also calibrate their network because the score given by the discriminator is often not reliable and cannot be treated as probabilities. Using an held-out set, they warp the output of the discriminator.

The method seems to help with the common mode collapse issue and can be used with any GAN architecture (DRS is a naive discriminator rejection sampling).

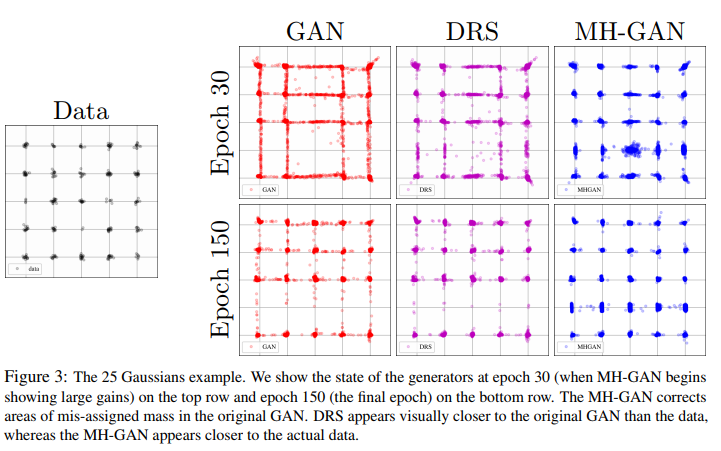
They do get better Inception scores :

Code

Blog