Introduction

The authors of the paper propose a novel way to counter catastrophic forgetting during sequential learning of GANs. They propose Memory Replay GANs (MeRGANs), a conditional GAN that integrates memory replay.

Sequential learning

The task proposed by the authors is to sequentially learn from a training set \(S = \{ S_1, ..., S_M\}\) where M is the number of categories. Each subset \(S_C\) represents the training set for a specific category and is considered a task t. The goal is to train a conditional GAN to generate images from all the sets after being trained on each set sequentially.

All methods use an AC-GAN framework with the WGAN-GP loss.

The generator’s parameters are denoted \(\theta^G\). The generator generates images according to \(\tilde{x} = G_{\theta^G}(z, c)\) where z is a latent vector and c is a category.

The discriminator’s parameters are denoted \(\theta^D\).

The AC-GAN uses a auxiliary classifier C whose parameters are denotes \(\theta^C\). The classifier predicts the image labels \(\tilde{c} = C_{\theta^C}(x)\)

The GAN’s parameters are denoted as \(\theta = (\theta^G, \theta^D, \theta^C)\) in the equations.

Previous Methods

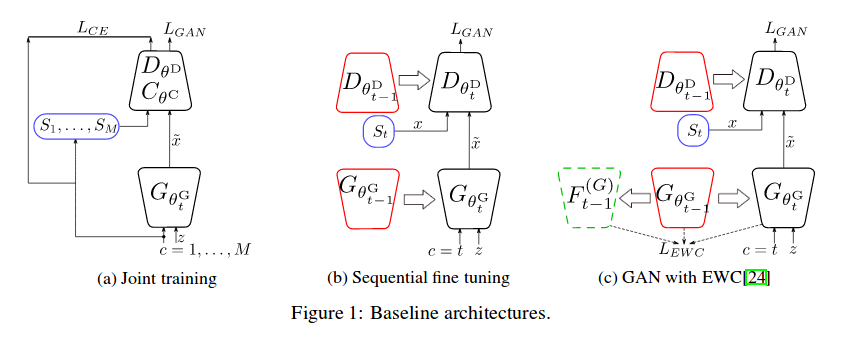
Joint learning

This method is not sequential learning, all categories are learned at the same time. The classical GAN optimization is used with WGAN modifications.

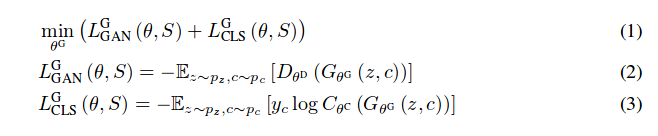
where \(L^G_{GAN}(\theta, s)\) and \(\lambda_{CLS}L^G_{CLS}(\theta, s)\) are GAN loss and cross-entropy loss. \(y_c\) is the one-hot encoding for the category c.

The category c is sampled uniformly and z is sampled from a Gaussian distribution.

The discriminator is trained according to the following equations:

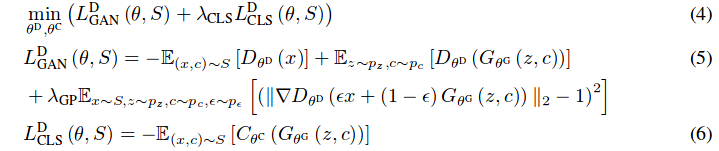
Sequential fine tuning

The authors define a sequence of T tasks, one for each category. They then train their GAN one task at a time. Each GAN is initialized with the previous GAN’s parameters.

Elastic Weight Consolidation

The authors present Elastic Weight Consolidation as a baseline for their new method to prevent forgetting. Elastic Weight Consolidation involves adding regularization to prevent the GAN’s parameters from changing too much during each task.

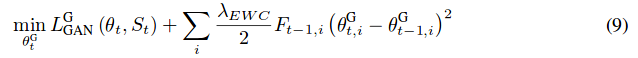
\(F_{t-1,i}\) is the Fisher information matrix that indicates how sensitive the parameter \(\theta^G_{t, i}\) is to forgeting.

Method

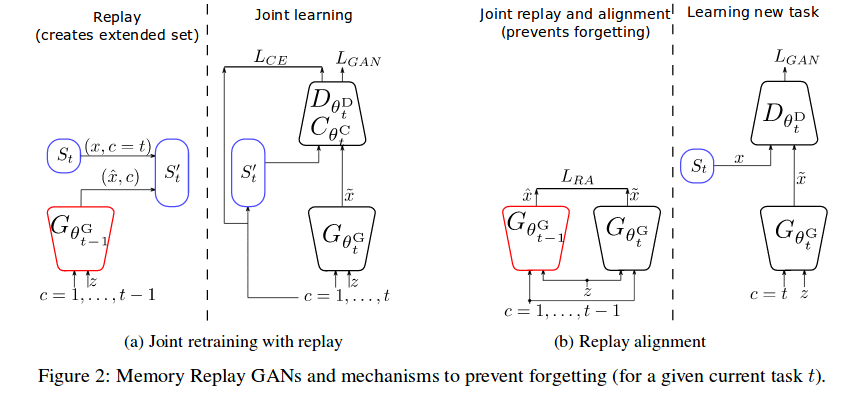
Joint retraining with replayed samples

Their first method involves extending the current task’s dataset with the memory from the previous task’s GAN. \(S_t' = S_c \cup_{c\in{1,...,t-1}} \tilde{S_c}\), where \(\tilde{S_c}\) is the replay set generated by \(\tilde{x} = G_{\theta^G_{t-1}}(z, c)\).

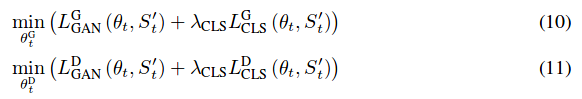
Replay alignment

The second method the authors propose involves adding a loss term for the generator. This loss term is an L2 loss between the current and previous GAN outputs for the same category c and latent vector z.

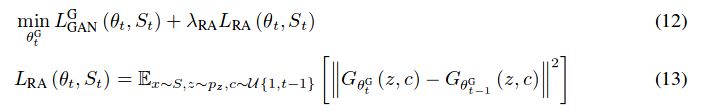
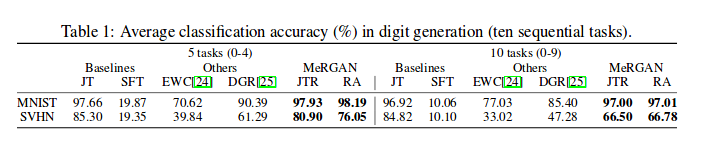
Results

The authors tested their two MeRGANs on digits generation with MNIST and SVHN and scene generation with 4 classes from the LSUN dataset. They compared their results to joint training, sequential fine tuning, Elastic Weight Consolidation and deep generative replay (Unconditional GAN with replay memory).

MNIST and SVHN

The authors trained a classifier on real data and used the classification accuracy on the generated data to evaluate forgetting.

LSUN

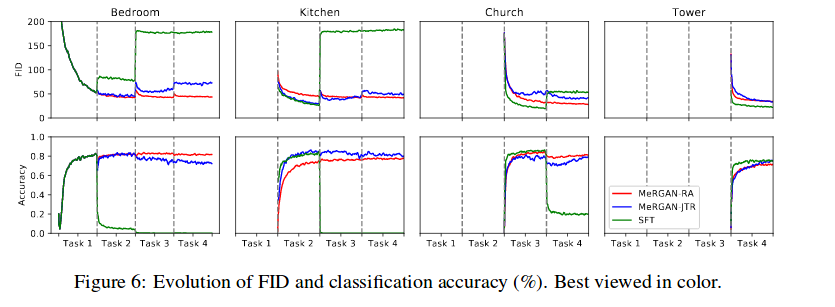
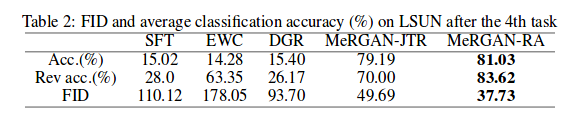
The authors used a classifier to evaluate forgetting. They tested a classifier trained on real data on generated data and a classifier trained on generated data on real data (Rev acc.). Finally, they tested the Frechet Inception Distance (FID) on the generated data.

Code: https://github.com/WuChenshen/MeRGAN

Video: https://www.youtube.com/watch?v=zOHrHrVq5C8&feature=youtu.be

Blog: http://www.lherranz.org/2018/10/29/mergans/