Highlights

The authors propose a novel and effective method based on a single trainable 3D convolution kernel that enables high quality results with a compact four-layer architecture and without sensitive hyperparameters for convolutions and architectural design. Their “one binary extremely large and inflecting sparse kernel” (OBELISK) automatically learns filter offsets in a differentiable continuous space together with weight coefficients.

They propose to use a simple coordinate transform geometric data augmentation strategy for the training.

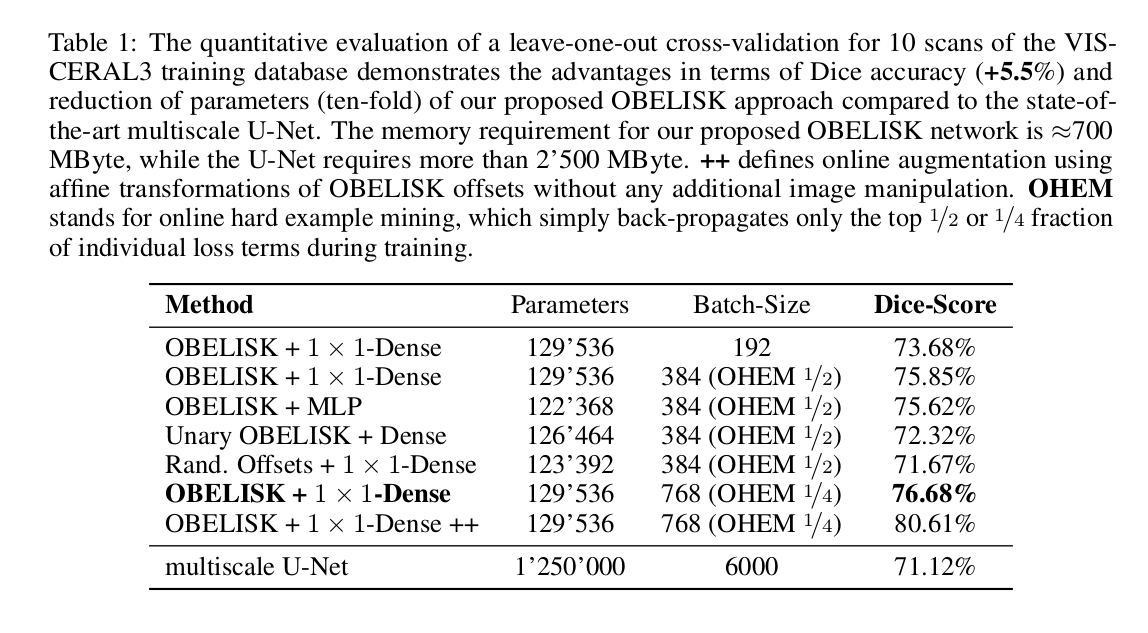
The architecture has less than \(130000\) parameters, can be trained in few minutes with only \(700\) MBytes of memory and achieves an increase of Dice overlap of \(+5.5\%\) compared to the U-Net for CT multi-organ segmentation.

The network trains on a reduced amount of annotated data.

Applied to multi-organ segmentation and image registration.

Introduction

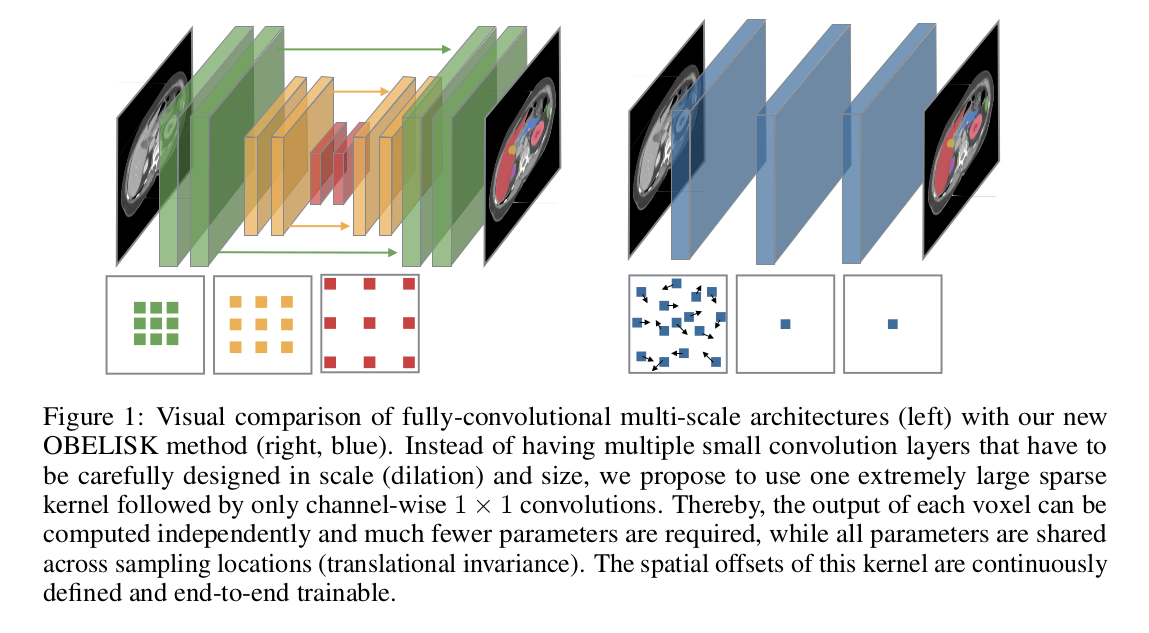
The specifications of a convolutional network are subject to much manual design. training 3D fully-convolutional multi-scale architectures with skip-connection that excel at semantic segmentation and landmark localisation have huge memory requirements and rely on large annotated dataset

Authors question the fundamental deep convolutional neural network common beliefs:

• More convolutional layers always lead to better results
• Small convolutional filters are preferable to larger ones
• Multi-scale or progressive dilated receptive field are necessary for dense prediction.

They propose a new single, binary kernel in which both the spatial offsets and coefficients are learned in a continuous, differentiable space.

Methods

• \(3\) layers; \(1\) sparse convolution followed by either a multi-layer perceptron (MLP) classifier or \(1 \times 1\) DenseNets.
• 4 kernels/channel.
• The spatial offsets of the kernels are continuously defined and are learnable.

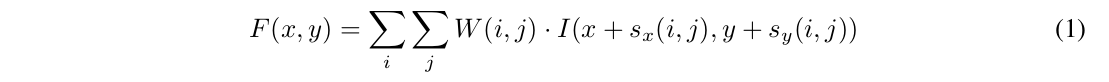
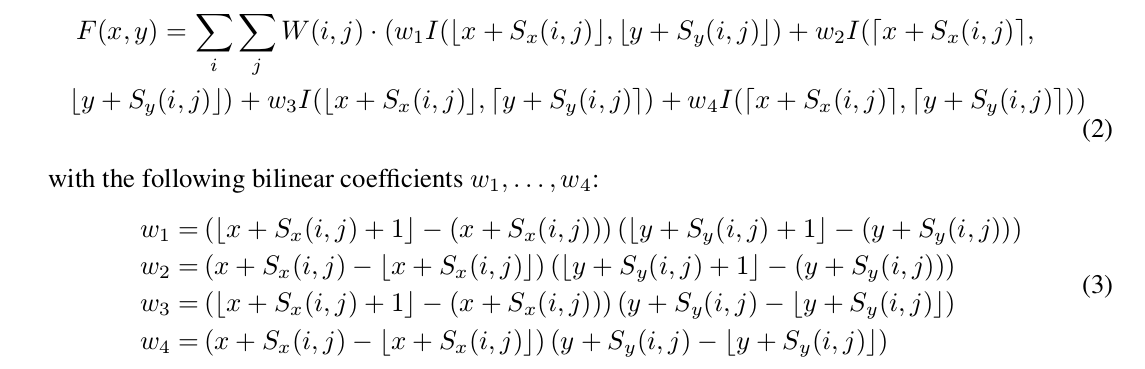
• They propose a binary extension that learns two offsets for each convolution element.
• Spatial offsets initialised with normally distributed random numbers.
• Due to the interpolation step, the image locations for which they draw labels and calculate the large convolution kernel can be on arbitrary continuous-valued coordinates. This enables them to use randomly selected patches across different images and locations that may be more diverse than the entire image batches used in FCNs.

• Leave-one-out validation.

Data

10 CT scans from the VISCERAL3 dataset¹. 7 classes.

Results

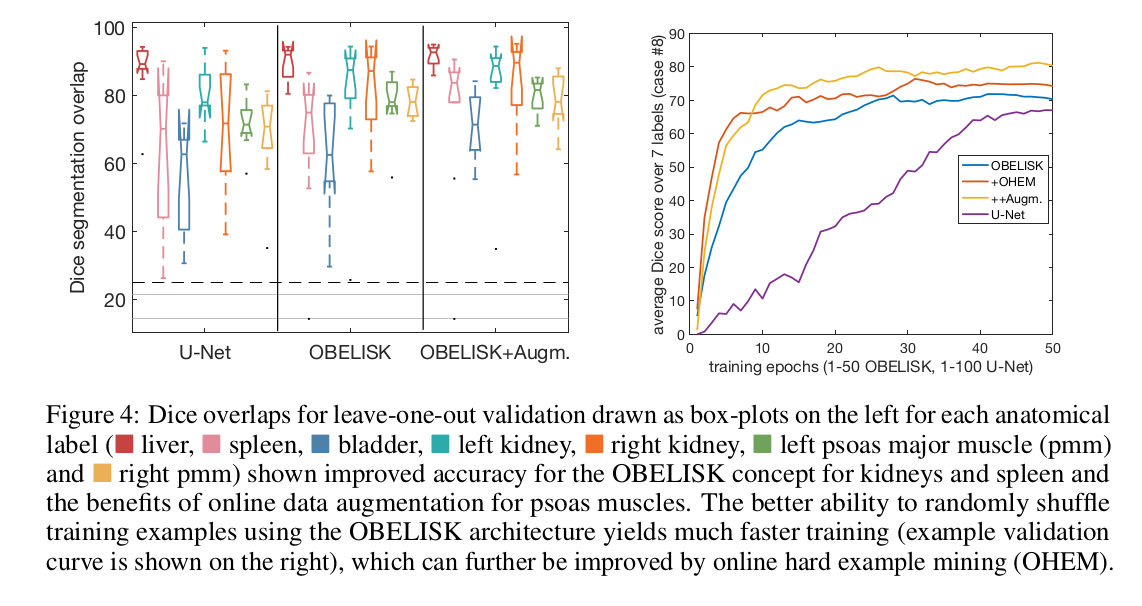
Multi-organ segmentation

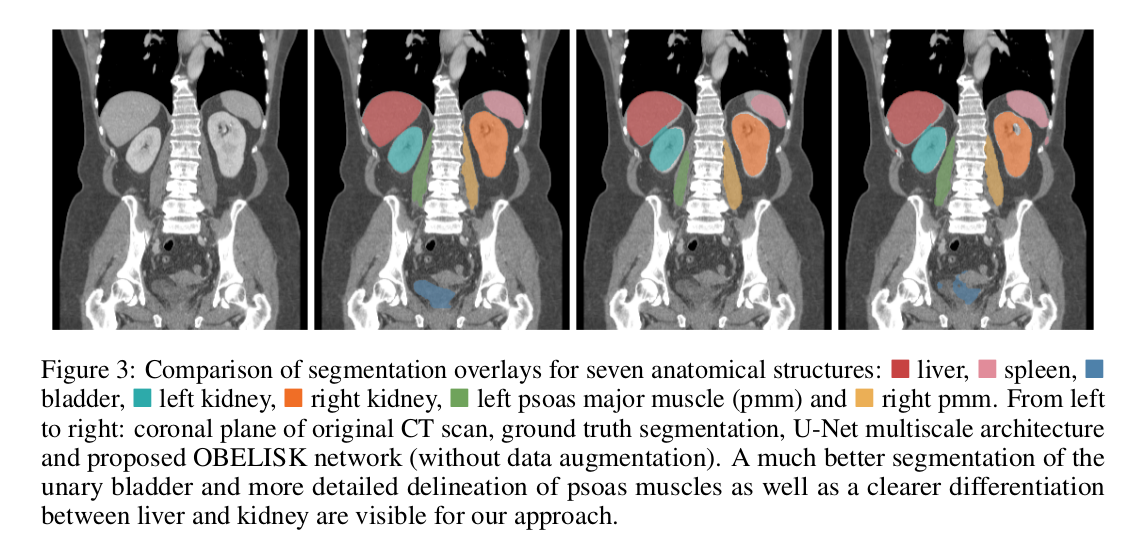
• Compared results to a U-Net architecture with 14 \(3 \times 3 \times 3\) convolutional layers and 8-128 channels.
• Improved convergence.
• Training using “online hard example mining”² improves results.
• Coordinate transform geometric data augmentation improves results.

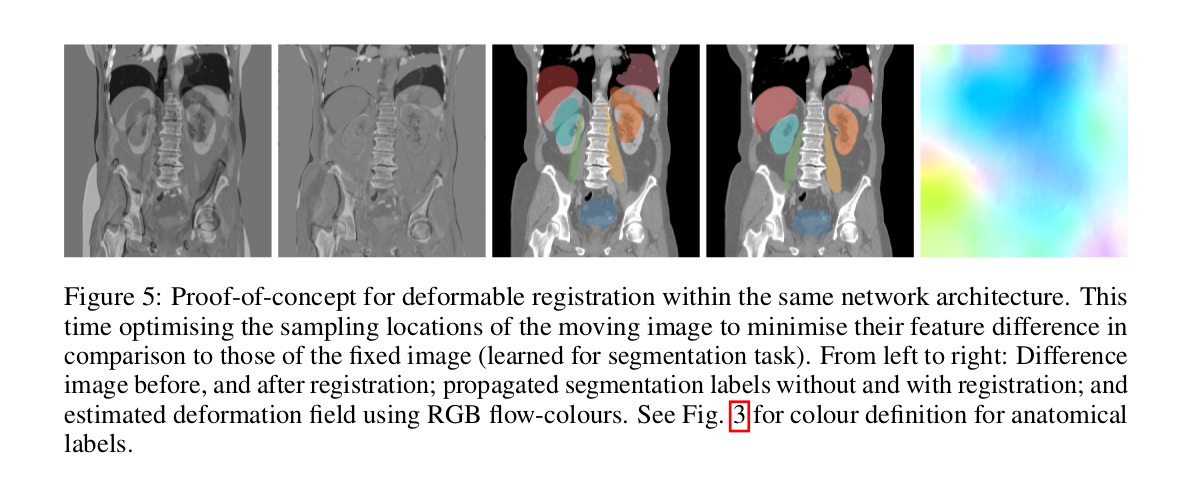
Registration

• Deformable (2D) registration based on the learned features (trained for a segmentation task).
• Changes to architecture: filter offsets and convolutional weights remain fixed, but minimise an \(L_1\) loss term (on the difference of feature vectors between fixed and moving image) by changing the sampling coordinates of the moving image. An additional penalty that penalises the difference between the estimated deformations and a B-spline filtered version of them is introduced to obtain smooth deformations.

Discussion

Their architecture outperforms 3D U-Nets by \(5.5\%\) Dice overlap for multi-organ segmentation while reducing the number of parameters by \(90\%\). Hence, they suggest that the three common requirements for CNN-based segmentation (deep networks, small kernels, multi-scale or dilation architecture) are not always necessarily the best choice.

They mention 3 main benefits:

• The architecture can deal “more naturally” with anisotropic high-dimensional data.
• Spatial locations for predictions can be adaptively sampled, which enables more variability in training batches.
• Features can be extracted with true translational invariance and for arbitrary positions, which can be beneficial for further tasks such as deformable registration.

Conclusions

• Spatial context is captured using a large kernel where offsets are learnt instead of using multiple layers.
• Sparsity in the kernels, much like \(L_1\) norm regularization would promote.
• Although they claim that their method can deal with anisotropic data, no results that support the claim are provided.
• Training times are decreased compared to U-Net, the inference for unseen data takes longer (\(13\times\)). Some limited experiments are presented in an attempt to overcome the issue.
• If sufficiently large annotated data and GPU resources are available, trying U-Net architectures may still be better than using OBELISK.

References