Automatically Designing CNN Architectures for Medical Image Segmentation
Introduction
The authors of this paper propose a new and simple technique to automatically design neural networks using policy gradients. The technique involves learning the optimal hyperparameters for an encoder-decoder network used for segmentation with the ACDC dataset. An optimal policy is found by iteratively perturbating a random policy and updating it with the perturbations that yielded the best reward (i.e. Dice index).
Method
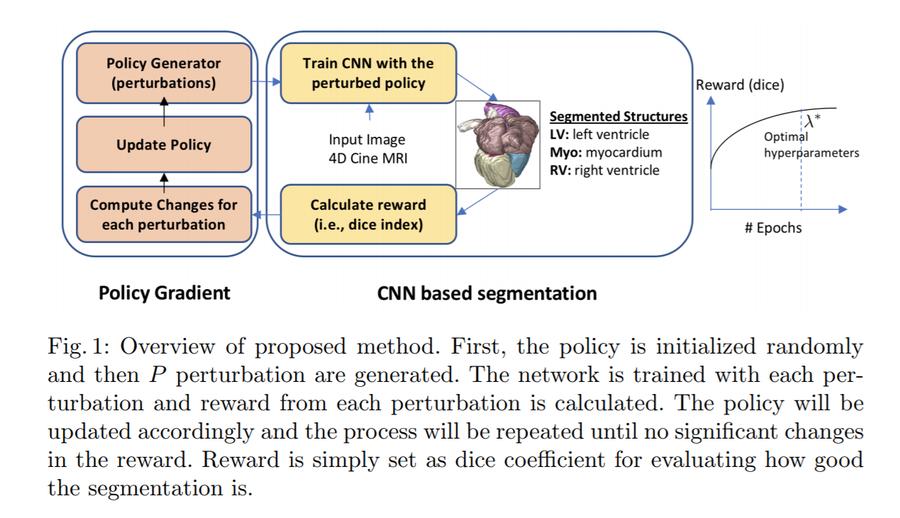
In this method, each hyperparameter is considered a policy. The method starts with a base policy, initialized randomly.
Assume this random policy as \(\pi_0 = \{\theta_1, \theta_2, ..., \theta_N\}\) indicating the hyperparamters of the network. N is the number of hyperparameters.
New policies are generated by applying random perturbations to the policy in each dimension (for each hyperparameter)
Let:
\[P(\pi_0) = \{\pi_1, \pi_2,..., \pi_p\}\]define p random perturbations near \(\pi_0\), where:
\[\pi_i = \pi_0 + \Delta_i \text{ for } i \in \{1, 2,..., p\}\]For each perturbation \(\pi_i\), \(\Delta_i\) is defined as:
\[\Delta_i = \{\delta^1, \delta^2,..., \delta^N\}\]where \(\delta^d\) is a randomly chosen from \(\{-\epsilon^d, 0, +\epsilon^d\}\) with \(d \in \{1, 2,..., N\}\). \(\epsilon\) is the derivative of a function \(y\) with respects to \(x\). These functions are the learnable hyperparameters for each layer:
- Number of filters: \(y_{NF} = 16x_{NF} + 16 \text{ with } x_{NF} = \{1, 2,..., 12\}\)
- Filter height: \(y_{FH} = 2x_{FH} + 1 \text{ with } x_{FH} = \{0, 1,..., 5\}\)
- Filter width: \(y_{FW} = 2x_{FW} + 1 \text{ with } x_{FW} = \{0, 1,..., 5\}\)
- Pooling function: \(y_{pooling} = x_{pooling} \text{ with } x_{pooling} = \{0, 1\}\) where 0 is maxpooling and 1 is average pooling.
The segmentation network is trained with the p generated policies and a reward is obtained from each policy.
To estimate the partial derivate of the policy function for each dimension (hyperparameter), each perturbation is grouped to non-overlapping categores of negative perturbations, zero perturbations and positive perturbations. \(C^d_-\), \(C^d_0\) and \(C^d_+\) such that \(\pi^d_i \in \{C^d_-, C^d_0, C^d_+\}\). This categorization is based on the perturbation that was applied in that dimension (\(\{-\epsilon^d, 0, +\epsilon^d\}\)).
Then, the absolute reward for each category is calculated as a mean of all the rewards \(Ave^d = \{Ave^d_-, Ave^d_0, Ave^d_+\}\) for each dimension d.
Finally, the initial policy is updated based on this average reward in the following way and the process is repeated:
\[\pi^d_{0, new} = \begin{cases} \pi^d_0 - \epsilon^d & \text{if } Ave^d_- > Ave^d_0 \text{ and } Ave^d_- > Ave^d_+ \\ \pi^d_0 + 0 & \text{if } Ave^d_0 \geq Ave^d_- \text{ and } Ave^d_0 \geq Ave^d_+ \\ \pi^d_0 + \epsilon^d & \text{if } Ave^d_- > Ave^d_0 \text{ and } Ave^d_- > Ave^d_+ \\ \end{cases}\]
Architecture
This method was tested using a new architecture presented by the authors: densely connected encoder-decoder CNN
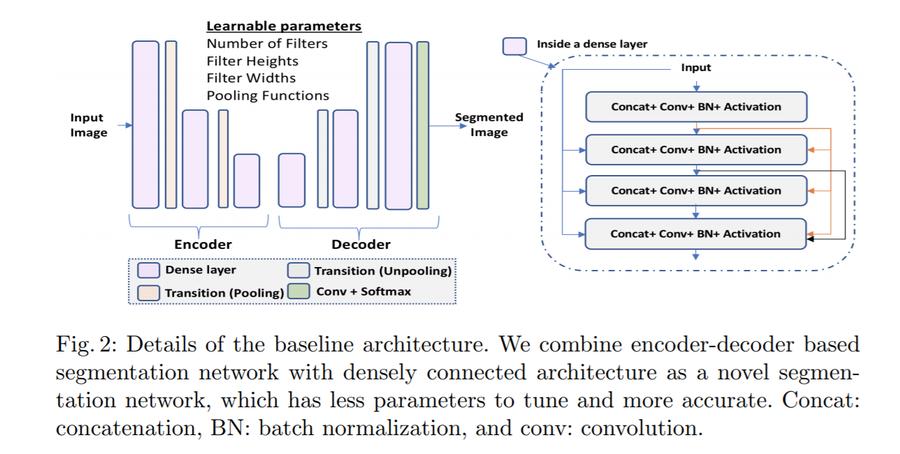
Each layer of this architecture is defined by the following equation:
\[F(X_l) = Conv(BN(Swish(X_l)))\]Because each layer is connected to all previous layers in this architecture, each layer is further defined as:
\[F(X_l) = F( \parallel_{l' = 0}^{l'=l-1} F(X_{l'})) \text{ for } l \geq 1 \text{ and } l = \{1, 2,...L\}\]where \(\parallel\) is the is the concatenation operation along the channel axis.
The encoder’s downsampling layers are either max or average pooling (learned by the policy gradient).
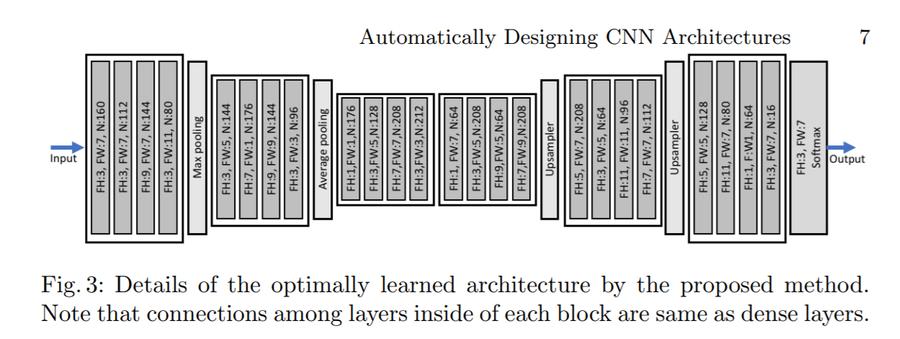
There are therefore 76 hyperparameters.
- 3 parameters for each of the 25 layers (the last layer has a fixed number of filters)
- 2 additional hyperparameters for the 2 pooling layers.
Experiments
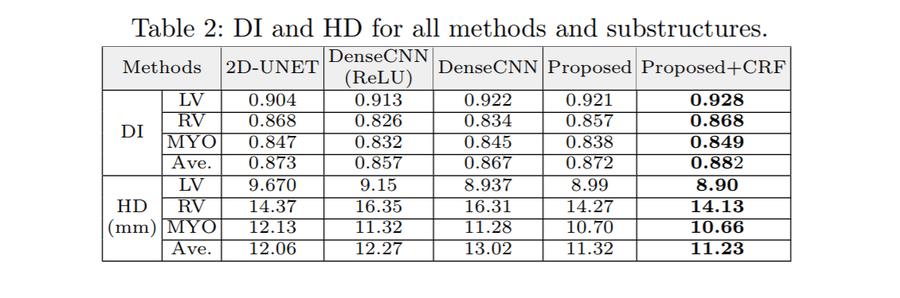
This method and architecture were tested on the ACDC dataset. The network was trained with an Adam optimizer with learning rate 0.0001 and a cross entropy loss. Each perturbated network was trained for 50 epochs in order to evaluate the reward (average over the last 5 epochs).
The authors used rotations and scaling to augment the data and a 3D fully connected Conditional Random Field (CRF) to refine their results.
The final learned hyperparameters are:
The method was trained on 15 Titan X GPUs for 10 days.