The idea

Deep reinforcement learning (DRL) has gained great success by learning directly from high-dimensional sensory inputs, yet is notorious for the lack of interpretability and the degenerate amount of trial-and-error necessary to provide interesting results. In this paper, the authors introduce symbolic planning into DRL and propose a framework of Symbolic Deep Reinforcement Learning (SDRL) that can handle both high-dimensional sensory inputs (pixels) and symbolic planning.

The method

The authors propose the following architecture:

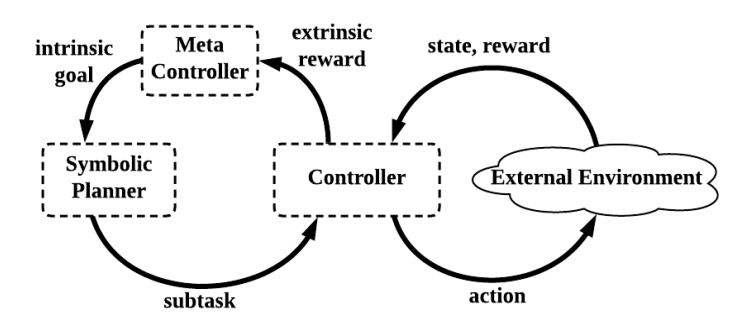
The planner uses prior symbolic knowledge to perform longterm planning by a sequence of symbolic actions (subtasks) that achieve its goals. The controller then uses DRL to learn a sub-policy for each sub-task. The meta-controller measures training performance of the controller and proposes new goals to the planner using standard reinforcement learning.

The planner uses actions and states defined in the Action Language BC1 and an “out-of-the-box” solver called Clingo2 to represent high-level states and actions which have preconditions and static conditions.

For example, here is the BC domain of Montezuma’s Revenge:

At any episode \(t\), the symbolic planner uses a logical representation \(D\), an initial state \(I\) and an intrinsic goal \(G\) (goal state) to generate a symbolic plan \(\Pi_t\). The transitions in \(\Pi_t\) each correspond to a sub-task and the controller uses Double-Deep Q Learning to learn a policy for each sub-task. Since rewards provided by the environment may be too sparse, an instrinsic reward is given to the agent. The intrinsic reward is defined as

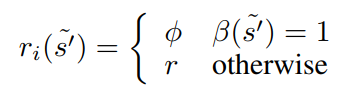
where \(\phi\) is a large number to encourage sub-task completion, \(\beta (s)\) means sub-task completion and \(r\) is the reward provided by the environment.

After the sub-task is completed or a pre-determined number of steps is reached, the success rate of the true environmental reward is used to define an extrinsic reward:

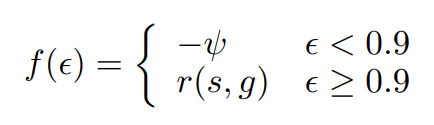
where \(\epsilon\) is the success rate of the sub-task, \(- \psi\) is a large number to punish unsolvable sub-tasks and \(r(s, g)\) is the true cumulative reward for the sub-task.

The meta controller then uses standard Q-Learning to evaluate the transitions between sub-tasks. An overall plan quality is then calculated and the results are passed back to the planner, which then tries to generate a better plan. The process is repeated until the plan cannot be further improved.

For completion’s sake, here is the full algorithm:

The results

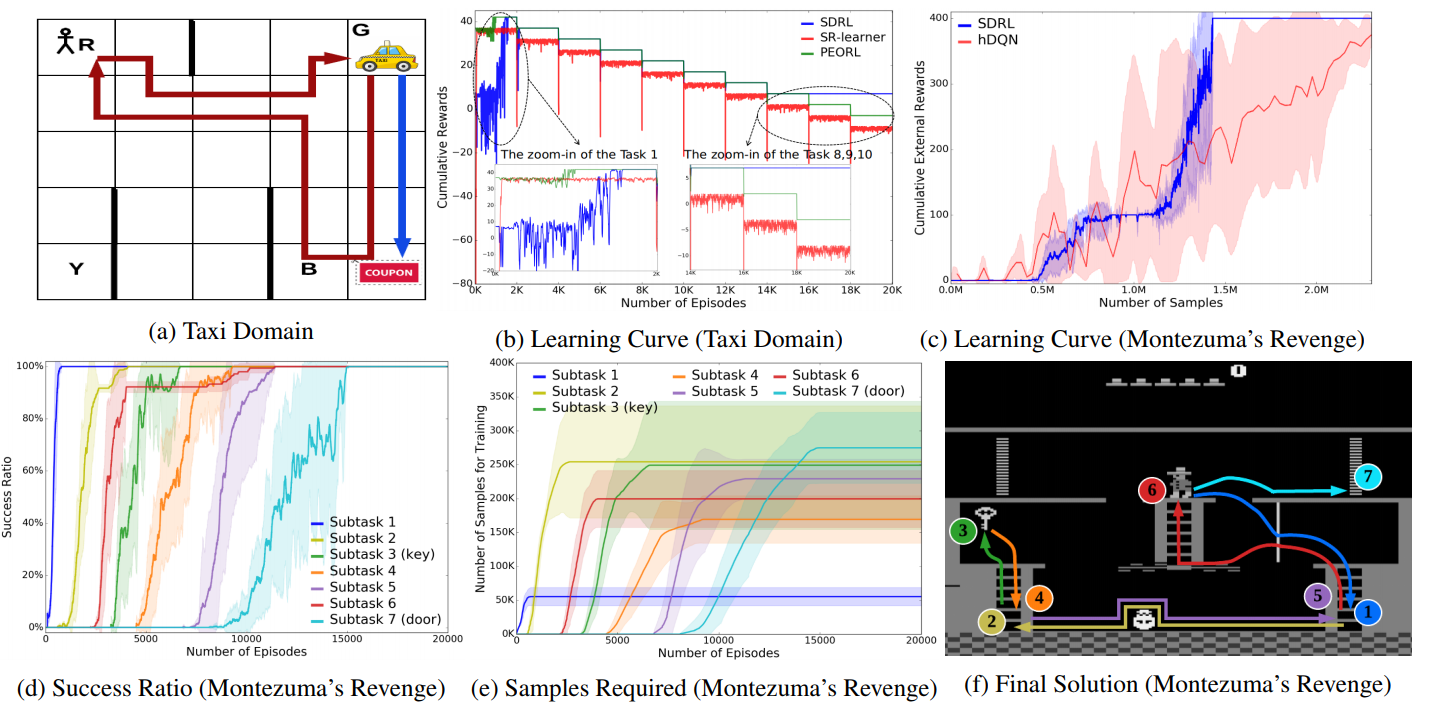
\((a)\) demonstrates the Taxi Domain game, \((b)\) shows that SDRL converges much faster and provides much better rewards than other algorithms. \((c)\) shows the reward and number of samples required versus Hierarchical Deep Q-Learning in Montezuma’s revenge and \((f)\) shows that the algorithm provides interpretable results.

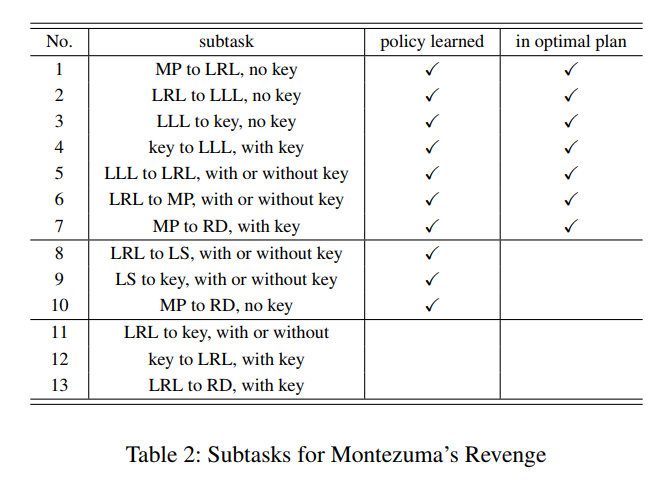
Here are the subtasks provided to the planner for Montezuma’s Revenge: