The authors propose an ADMM approach for performing unstructured pruning with a sparsity factor target.

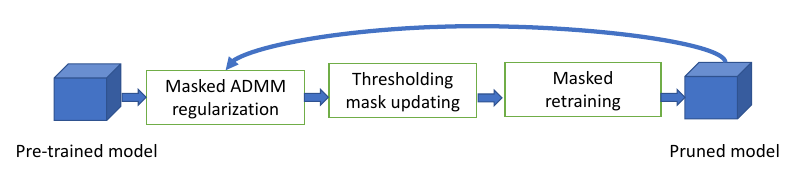
Overall framework

They combine ADMM regularization and masked retraining into a 3-step iterative process:

ADMM formulation

In the following, f() is the loss function, W and b are the weights and biases respectively.

Here are the 2 sub problems:

The first is simply the DNN training, but with a special regularizer:

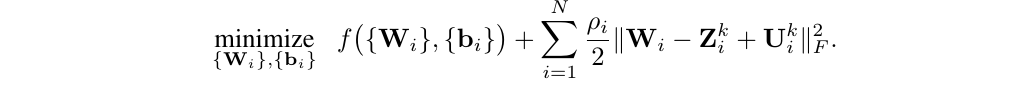
The second has the goal of projecting the current network structure into the set of correct structures (the set of neural networks which have the required sparsity factor):

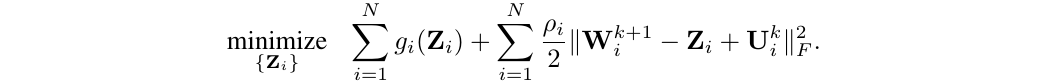
This last optimization problem can be solved with following operation: leave intact the top-k weights (by magnitude), and zero-out the others, where k is the number of weights corresponding to the required sparsity. This operation is conducted in a layer-wise fashion.

Masked Retraining

At high compression rates, the ADMM method alone is not sufficient, as it leaves too many weights near-zero, without being exactly zero. Their remedy is to alternate between ADMM training and masked retraining. Masked retraining consists in training the network that results from ADMM, this time with a traditional loss and while zeroing-out the parameter updates of the weights that have been pruned by ADMM.

Progressive Pruning

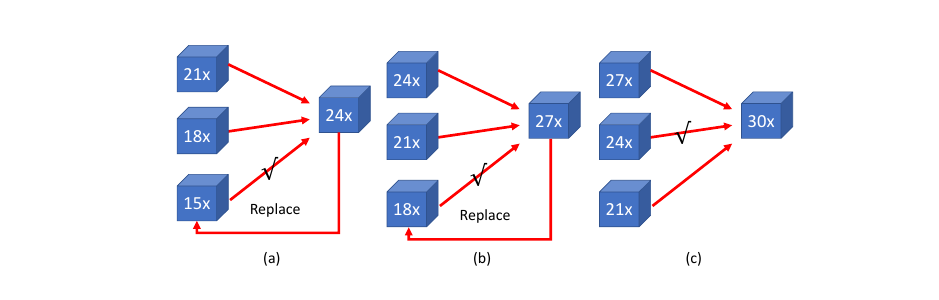
They use a rather weird progressive approach. To target a pruning ratio, they work in increments of 3x. They keep the three best architecture in terms of accuracy (they could have 15x, 18x, and 21x sparsity). From these, they try to prune further (say 24x). Of the three, the network that resulted in the next pruned network with the best accuracy is replaced by the new network (for example, the 15x gave the best 24x; and the 15x is replaced by this 24x). See the figure below for an example.

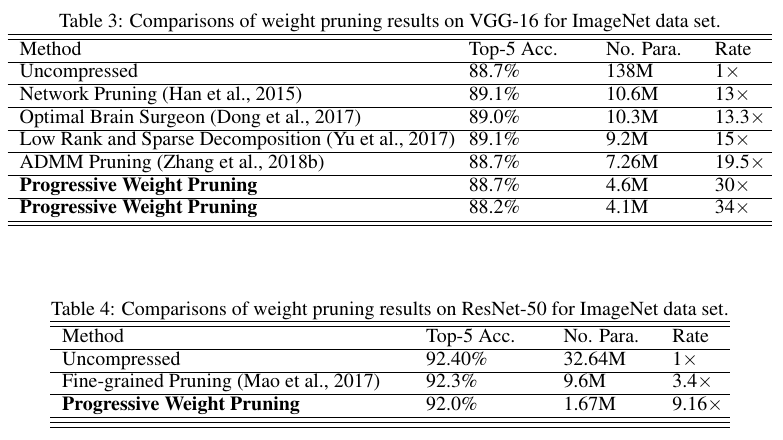
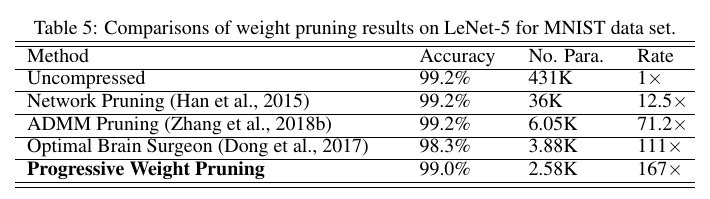
Results

Results are good. But since this is unstructured pruning, it will not result in acceleration (unless sparse matrix storage and operations are used).