In this paper, the authors examine the concept of residual connections through the lens of incremental/iterative inference.

ResBlocks: “Refinement” blocks?

It makes a lot of sense to view resblocks as “refinement” blocks. Let me explain. The typical way of illustrating resblocks is the following. (For simplicity, let’s ignore the spatial dimensions, and use only one layer per block):

In my opinion, this is misleading. The residual connections seem to be a “bonus”, just something you add to any good old feedforward network. Here is an illustration that I think is more representative:

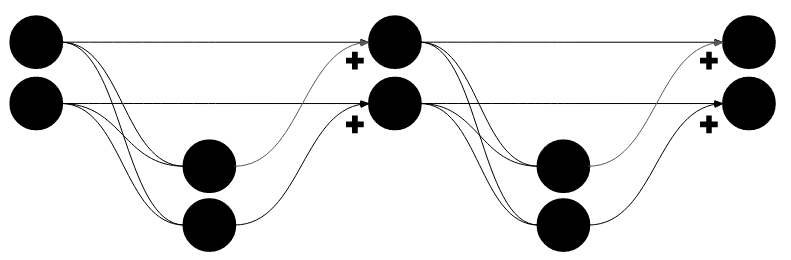
Same network, different interpretation. Here, the residual connections are drawn as straight lines, highlighting the continuity of the features throughout the layers. Now, the residual branch becomes the “main branch”, and the secondary branch computes a “delta” that “refines” the existing signal. This illustration also highlights the fact that a ResBlock does not (generally) change the number of features (or change the spatial dimensions) of the main signal.

Iterative refinement in ResNets

The authors provide 3 interesting contributions:

  1. They find that residual blocks are encouraged to produce deltas that are in the direction of the negative loss gradient. They empirically confirm this by comparing (with cosine distance) the delta produced by a resblock and the gradient of the loss relative to the hidden features prior to the block.

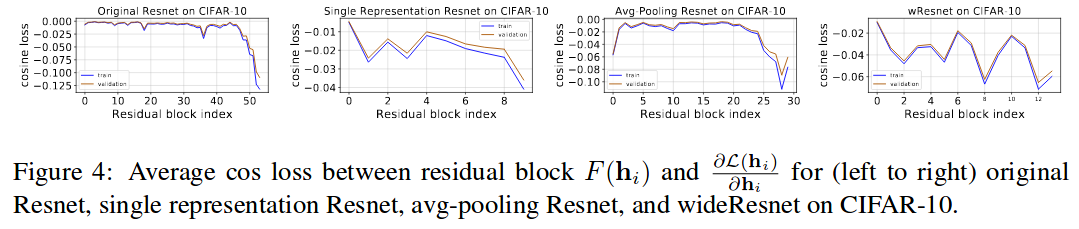
  2. They observe that resnets can perform both hierarchical representation learning and iterative feature refinement. They find that lower layers focus on representation learning, and upper layers on refinement. Since the upper layers are only refining, they can be removed with minimal effect on the accuracy.

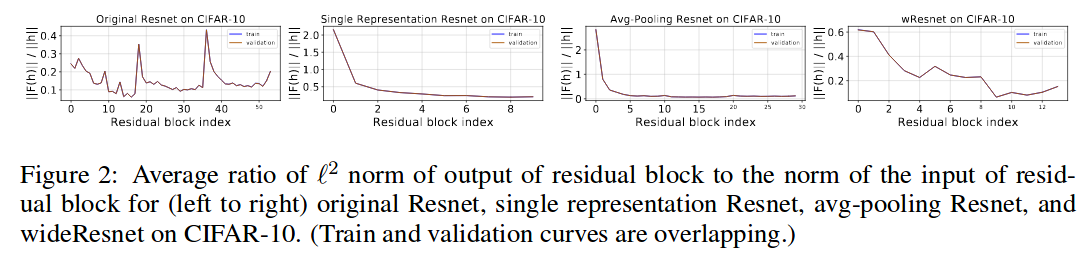
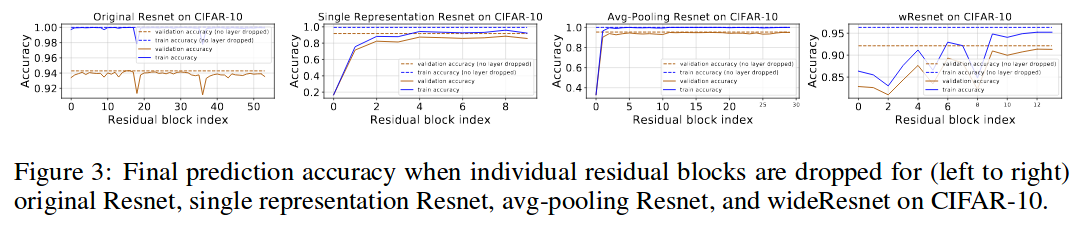
  3. They find a method for reusing resblocks, thus obtaining truly iterative inference. By sharing the parameters of the resblocks, we obtain an iterative application of the same transform; and it reduces the parameter count. But naively sharing parameters in a Resnet leads to bad performance. The authors propose a way to overcome this issue; but sadly good results are obtained when matching the number of parameters of the non-iterative baseline.

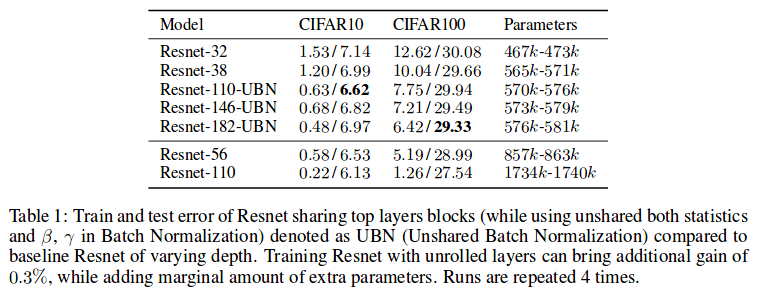
    Notice the horizontal line in the table that conveniently allows them to consider their method superior.