The idea

Problems that exhibit high initial station variation produce high variance policy-gradient estimates and are hard to solve via direct policy or value function optimization. This paper provides a novel algorithm that partitions the initial state into “slices” and optimizes an ensemble of policies over these slices, which are then unified into a central policy.

The method

Initial states are sampled and then clustered using k-means into contexts \(\omega_i\), each associated with a policy \(\pi_i(s,a) = \pi((\omega_i,s),a)\). A central policy is defined as \(\pi_c(s,a)=\sum _{\omega\in\Omega} p({\omega}{\mid}s) \pi_{\omega} (s,a)\) Each policy should stay as close to the central policy as possible by maximizing \(\eta(\pi_i) - \alpha \mathbb{E}[D_{KL}(\pi_i{\mid}{\mid}\pi_c)] {\forall i}\). They also want to keep the divergence between policies w.r.t

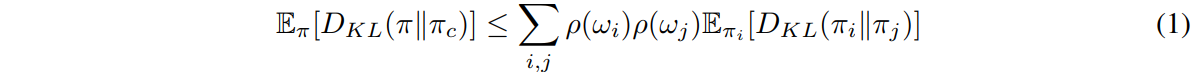
To update the policies, the authors use the following loss, devired from TRPO1:

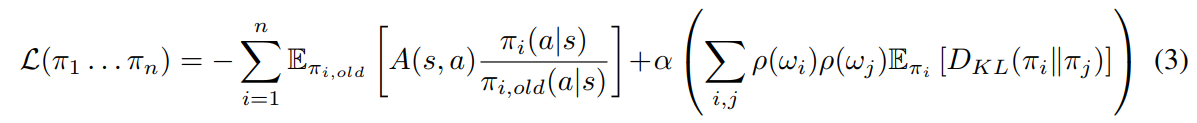
Then, the central policy is updated (the authors call this the “distillation step”):

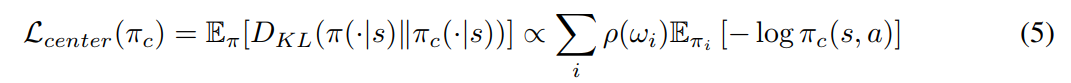
Finally, here is the full algorithm:

The results

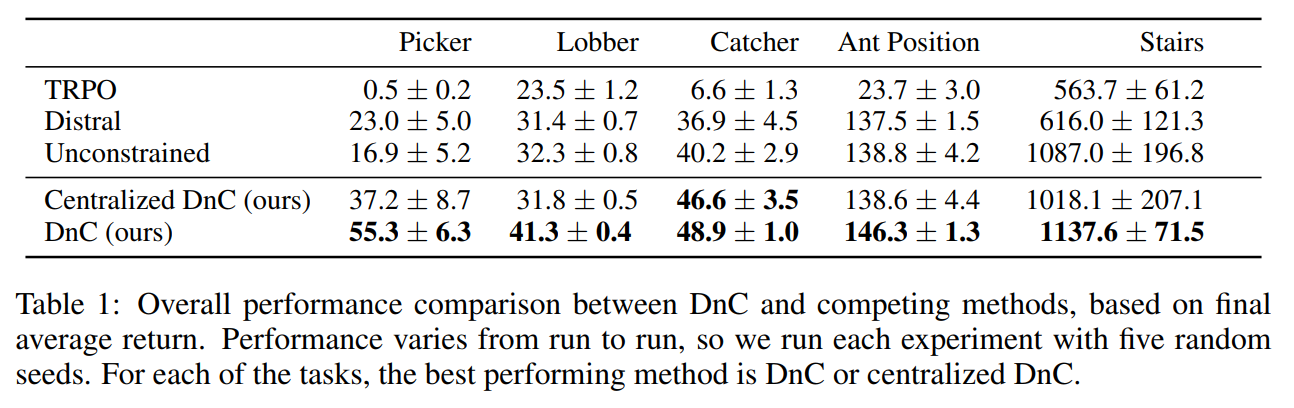
  • TRPO is considered state of the art in reinforcement learning Distral is another RL algorithm that splits the context, but uses a central policy learned through supervised learning
  • Unconstrained DnC means that DnC is executed without KL constraints. This reduces to running TRPO on local policies.
  • Centralized DnC is like running Distral but still updating the central algorithm.
  • Picking requires the robotic arm to pick up a randomly-placed block and lift it as high as possible
  • Lobbing requires picking a block and “lobbing” it in a randomly placed square
  • Catching requires the arm to catch a ball that is thrown at it at a random velocity and initial position
  • Ant requires controlling an ant to walk to a random flagged position
  • Stairs requires a bipedal robot to climb a set of stairs of varying heights and lengths

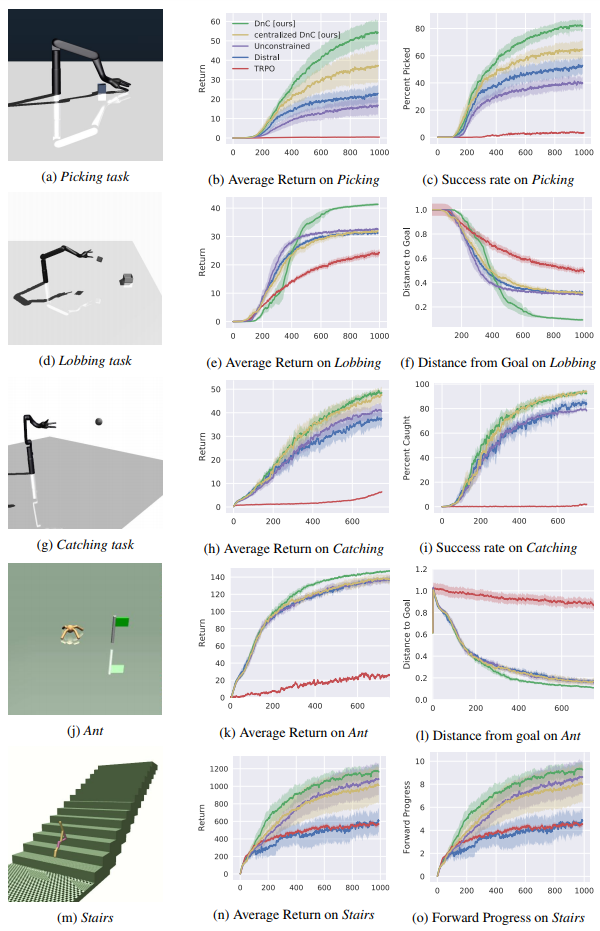
Finally, here’s a video of DnC versus TRPO