Highlights

A generalized loss function based on the Tversky index to address the issue of data imbalance is proposed.
A better trade-off between precision and recall in training 3D fully convolutional deep neural networks for multiple sclerosis lesion segmentation on magnetic resonance images.

Summary

In order to weigh FNs more than FPs in training the network for highly imbalanced data, where detecting small lesions is crucial, a loss layer based on the Tversky index is proposed.

Introduction

Data imbalance is a common issue in medical image segmentation.

Without balancing the labels the learning process may converge to local minima of a sub-optimal loss function, thus predictions may strongly bias towards non-lesion tissue. The outcome will be high-precision, low-recall segmentations.

A common approach to account for data imbalance, especially in voxel-wise methods, is to extract equal training samples from each class. The downsides of this approach are that it does not use all the information content of the images and may bias towards rare classes.

Other strategies have proposed work well for relatively unbalanced data like brain extraction or tumor segmentation, but the perform less well in highly unbalanced data tasks, such as multiple sclerosis lesion segmentation.

Tversky index is a generalization of the Dice similarity coefficient and the $$F_{\beta} scores.

Methods

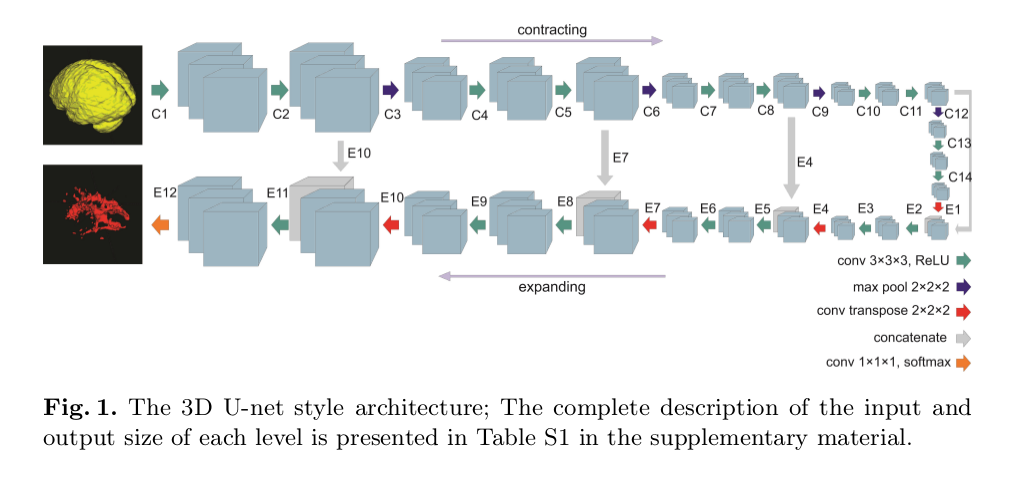
Architecture: U-Net

Tversky index

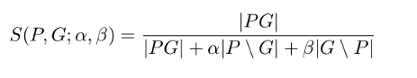
where $P$ and $G$ are the set of predicted and ground truth binary labels, respectively, and $\alpha$ and $\beta$ control the magnitude of penalties for FPs and FNs, respectively.

Loss function

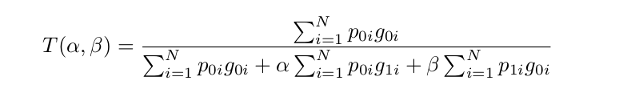
where in the output of the softmax layer, the $p_{0i}$ is the probability of voxel $i$ be a lesion and $p_{1i}$ is the probability of voxel $i$ be a non-lesion. Also, $g_{0i}$ is $1$4 for a lesion voxel and$0$for a non-lesion voxel and vice versa for the$g_{1i}$$.

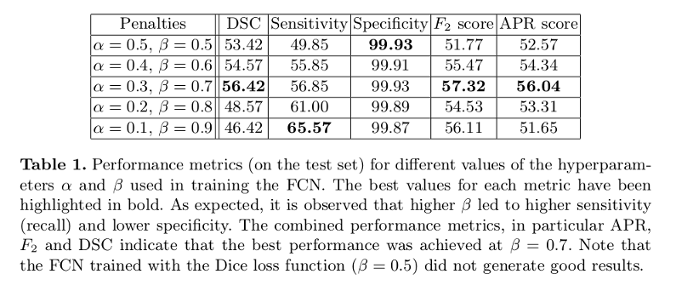
Metrics

Dice similarity coefficient (DSC) ($2TP/(2TP + FP + FN)$)
Sensitivity (recall, $TP/(TP + FN)$)
Specificity ($TN/(TN + FP)$)
F2 score ($5TP/(5TP + 4FN + FP)$)
APR score (area under the Precision-Recall curve)

Data and Parameters

T1- and T2-weighed FLAIR MRIs of 15 subjects
Rigid registration to a reference at size $128 x 224 x 256$
Two-fold cross-validation
Adam optimizer
Learning rate of $0.0001$ with a decay factor of $0.9$ every $1000$ epochs

Results

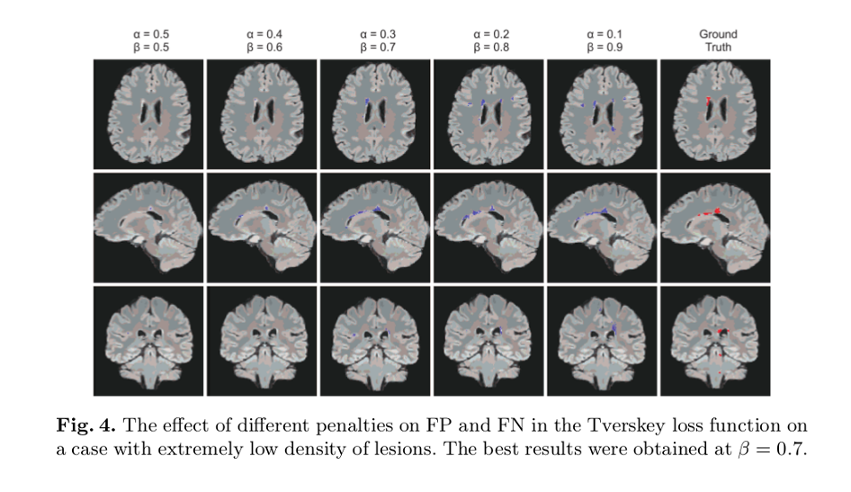
Adjusting the hyperparameters of this Tversky index allow placing emphasis on false negatives in training a network that generalizes and performs well in highly imbalanced data
Outperforms Dice index-based loss results
Training: 4 hours (NVIDIA GeForce GTX1080 GPU)