Binarized Neural Networks
Summary
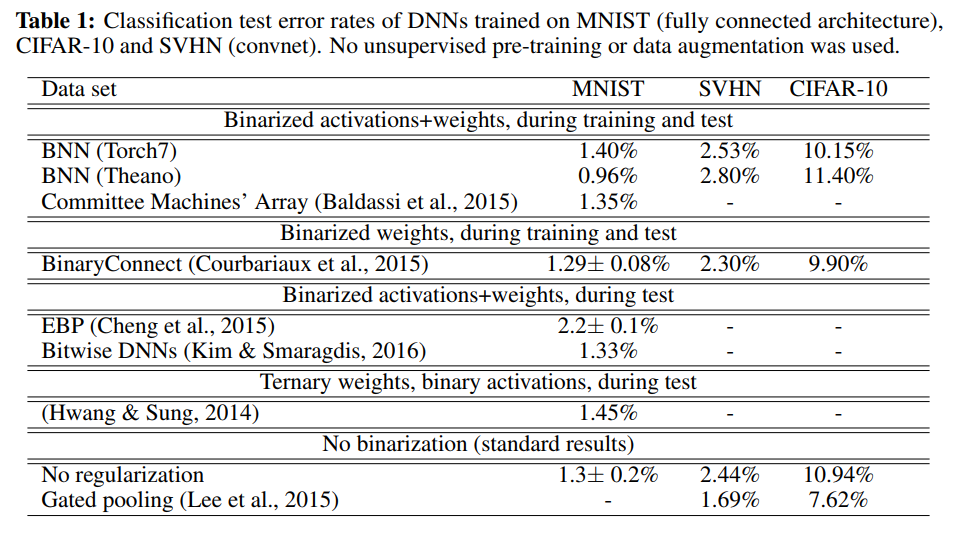
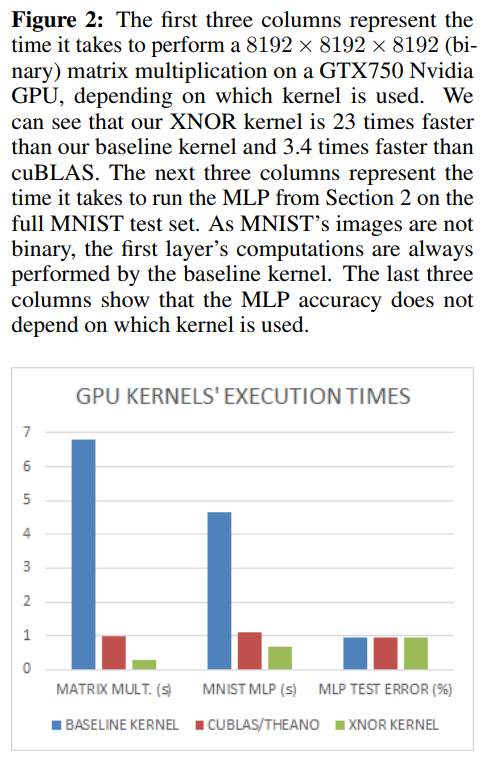
BNNs achieved nearly state-of-the-art results over the MNIST, CIFAR-10 and SVHN datasets We wrote a binary matrix multiplication GPU kernel with which it is possible to run our MNIST BNN 7 times faster than with an unoptimized GPU kernel, without suffering any loss in classification accuracy.
Goal :
- Binarize weights and activations
- Be more efficient:
most of the 32-bit floating point multiply-accumulations are replaced by 1-bit XNOR-count operations
- Use less memory:
In comparison with 32-bit DNNs, BNNs require 32 times smaller memory size and 32 times fewer memory accesses
Deterministic vs. stochastic binarization
Deterministic :
\[x^b = \text{sign}(x) = \begin{cases} +1 \text{ if } x >= 0, \\ -1 \text{ otherwise} \end{cases}\]Stochastic :
\[x^b = \begin{cases} +1 \text{ with probability } p = \sigma(x), \\ -1 \text{ with probability } 1 - p \end{cases};\] \[\text{ where } \sigma(x) = \text{clip}(\frac{x+1}{2}, 0, 1) = \max(0, \min(1, \frac{x+1}{2}))\]- Note: Stochastic binarization should be better than deterministic binarization, but is harder to implement since it requires random bits.
Training and gradients
-
Real-valued gradients of the weights and activations are stored during training for SGD to work.
-
The derivative of the sign function is zero almost everywhere, so the gradient cannot be used as is. Instead, a straight-through estimator is used, which corresponds to computing the gradient of the hard tanh: \(\text{Htanh}(x) = \text{clip}(x, -1, 1)\)
-
For better efficiency, Shift-based BatchNorm is used, which is an approximation of BatchNorm that uses almost no multiplications.

Experiments
- MNIST
- CIFAR-10
- SVHN
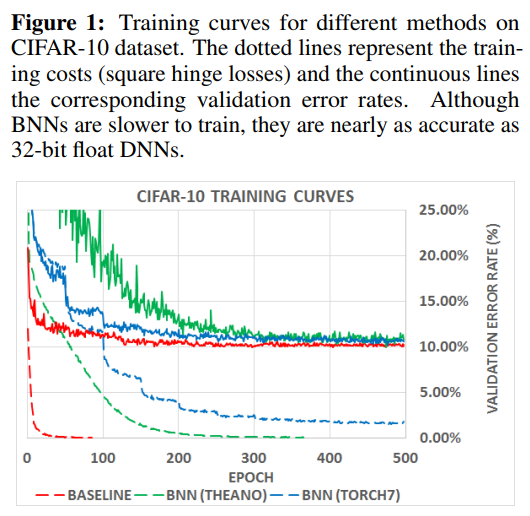
BNNs take longer to train, but are nearly as accurate:
New binary kernel is 7x faster on GPU: