Main Idea

Refine the predictions of structured prediction models by effectively integrating discriminative models into the prediction (normally it’s two separate networks).

Discriminative models are treated as energy-based models. They are trained to estimate scores which measure the quality of predicted outputs, while structured prediction models are trained to predict contrastive outputs with maximal energy scores. In this way, the gradient vanishing problem is improved, and inference is performed by following the ascent gradient directions of discriminative models to refine structured prediction models. The proposed method can handle a multi-label classification and image segmentation.

APPROACH

Discriminators and structured prediction models are respectively learned by optimizing:

\[\min_{\theta_{d}}\;\mathbb{E}_{x\sim px}[\dfrac{1}{2}(D(x, G(x;\theta_g);\theta_d)-v_g^{\ast})^2]\;+\;\mathbb{E}_{x\sim px}[\dfrac{1}{2}(D(x, y^{\ast};\theta_d)-1)^2]\]

Here \(v_g^{\ast} = v^{\ast}(G(x;\theta_g), y^{\ast})\).

It learns an energy-based model using training samples that consist of ground-truth samples \((x, y^{\ast} , 1)\) and predicted samples \((x, G(x;\theta_g ), v_g^{\ast})\). The discriminators are learned to predict oracle values \(v_g^{\ast}\) for the samples predicted by structured prediction models.

\[\min_{\theta_{g}}\;\mathbb{E}_{x\sim px}[L_g(G(x;\theta_g),y^{\ast})\;+\;\dfrac{1}{2}(D(x, G(x;\theta_g);\theta_d)-1)^2]\]

This equation regularizes structured prediction models such that the predicted samples tend to have higher scores.

After training, the discriminators can refine structured prediction models by utilizing a gradient-based inference. The outputs predicted by structured prediction models are updated following the ascent gradient directions of discriminators that lead to the high scores:

\[y^{(0)}\;=\;G(x;\theta_g)\] \[y^{(t+1)}\;=\;P_y (y^{(t)})+\eta \dfrac{(\dfrac{\partial}{\partial y}D(x,y^{(t)};\theta_d))}{\parallel \dfrac{\partial}{\partial y}D(x,y^{(t)};\theta_d)\parallel}\]

\(P_y\) denotes an operator that projects the predicted outputs back to the feasible set of solutions. The normalized gradient method is used to improve the predicted outputs and overcome the small-gradient issue.

Two different methods are used to generate training samples:

  • Inference samples: At each training iteration, structured prediction models are first used to predict samples. Take these samples as initial solutions and run a gradient-based inference to find high-valued samples of discriminators. These samples are useful since they are generated along the inference trajectory at the inference stage.

  • Adversarial samples: Maximize the loss \(\dfrac{1}{2}(D(x, y;\theta_d)-v^{\ast})^2\) with respect to \(y\) using a gradient-based optimizer. These samples serve as negative samples to learn discriminators.

EXPERIMENTS

Experiments are conducted on three tasks: multi-label classification, binary image segmentation, and 3-class face segmentation

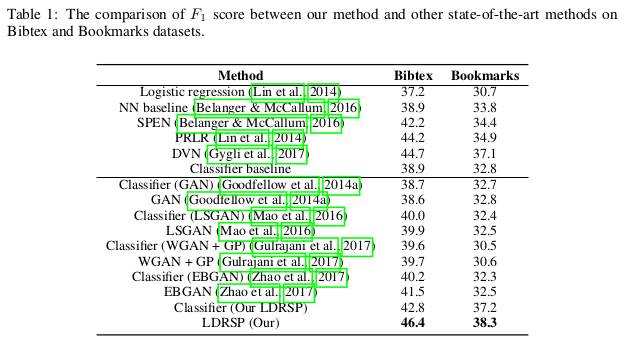
MULTI-LABEL CLASSIFICATION

On these two datasets, tags need to be predicted for text inputs, and multiple labels are possible for each input.

Classifier: two-layer neural network.

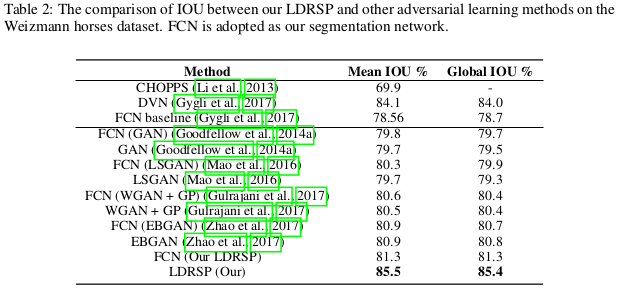
BINARY IMAGE SEGMENTATION

Classifier: fully convolutional network (FCN).

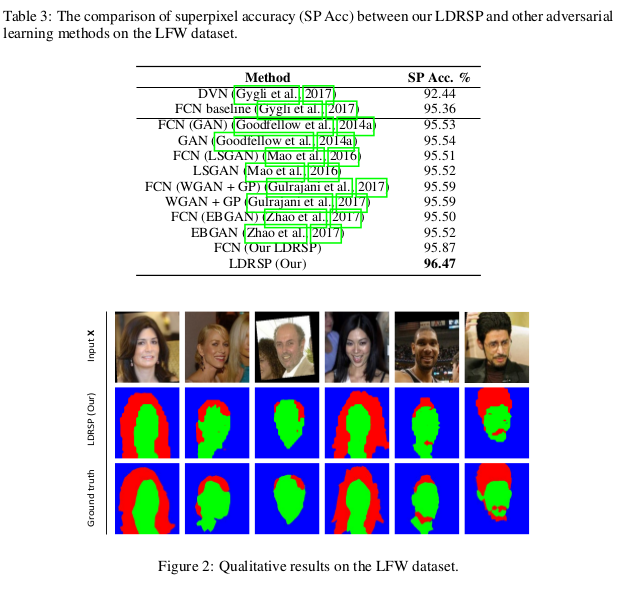
3-CLASS FACE SEGMENTATION

Classifier: fully convolutional network (FCN).