The authors aim to reduce the number of free parameters in neural networks. In the best cases, they can predict 95% of the parameters of a network, instead of learning them. Even then, no drop in accuracy is observed. This work is motivated by the Gabor-like smoothness of large filters learned in the first layer of a CNN.

Regression of the filter values

The authors propose to do a regression to map the coordinates of an image patch to the values in the filter. A possible choice of regression is a linear combination of basis functions. Let’s factorize the weight matrix:

\[W = UV\]

In this view, the columns of \(U\) are a dictionnary of basis functions, and the rows of \(V\) are the parameters of linear combinations of these functions. The advantage of this factorization is the small number of basis functions in \(U\), compared to the number of filters in \(W\). Several methods for building a dictionnary are proposed.

Choice of dictionnary

• Train a single-layer unsupervised model and use the learned features as a dictionnary.
• Use Fourier or wavelet bases.
• Use kernel ridge regression to predict filter weights from a small subset of known weights values. A good kernel for first-layer features is the exponential kernel, since natural images are smooth.

Kernel ridge regression

We can predict the whole filter \(\mathbf{w}\) using a subset \(\mathbf{w}_{\alpha}\) of the weights (the subset is chosen with a random uniform distribution over the spatial dimensions of the image patch):

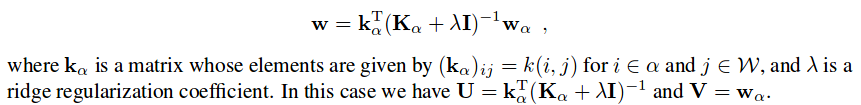
The subset of seen weights \(\mathbf{w}_{\alpha}\) is obtained by pre-training a single-layer autoencoder for each layer. The network is then trained end-to-end.

Experiments

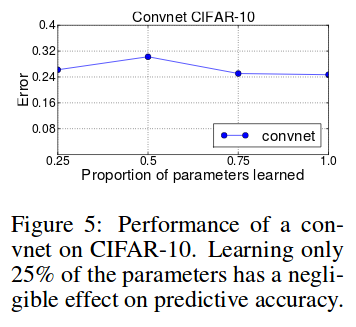
They experiment on MNIST with a 784–500–500–10 MLP and on CIFAR-10 with a LeNet. They do not predict the parameters of the classification layer.

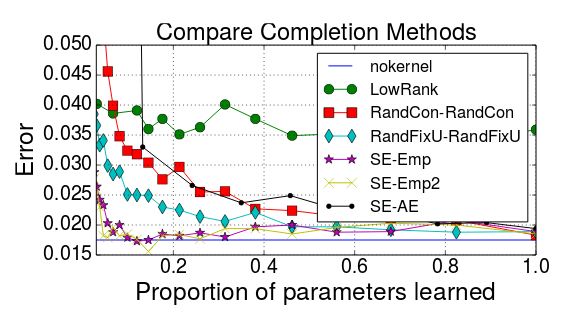
SE stands for “squared exponential” kernel.

Discussion

They consider LeNet to be a deep network, which is laughable nowadays. It’s unclear whether the findings presented in this paper apply to more recent, really deep networks. Anyways, it’s good to keep in mind that in a filter, which is a full grid, not all values are essential to describe the whole.