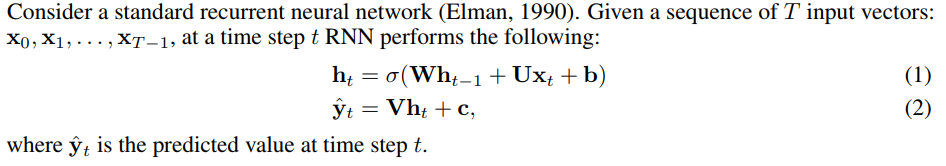Kronecker Recurrent Units
Summary
Goals
- Better weight efficiency
- Better conditioning of the recurrent weight matrix (prevent vanishing/exploding gradients)
Reminder: Vanilla RNN
Core idea
Factorize the NxN recurrent matrix using a Kronecker factorization. This allows some flexibility in the actual number of parameters through the size of the factors.
For example, using 2x2 factors, there are \(O(\log(N))\) parameters, whereas it can go up to \(O(N^2)\) parameters when using a single NxN factor (the original RNN description).
The vanishing and exploding gradient problem is tackled through a soft unitary constraint, which is easier to apply when using small factors.
NOTE: This soft constraint is not needed when using an LSTM, since the gating mechanism is already designed to prevent exploding/vanishing gradients.
Reminder: Kronecker product
Reminder: Unitary matrix
In real space, a unitary matrix is simply an orthogonoal matrix, i.e. its transpose is also its inverse:
\[Q^T Q = QQ^t = I \Leftrightarrow Q^T = Q^{-1}\]
In complex space, a matrix is unitary if its conjugate transpose is also its inverse:
\[U^* U = UU^* = I\]
(Remember, the conjugate transpose is the transpose matrix where the imaginary parts have their sign reversed.)
Factorization
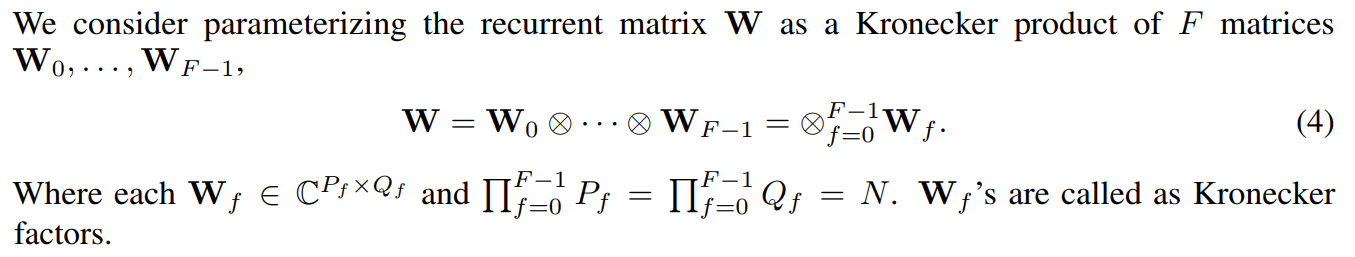
If factors are 2 x 2, then there are \(\log_2 N\) factors, the number of parameters is \(8 \log_2 N\) (when using complex factors), and the time complexity of the hidden state computation is \(O(N \log_2 N)\).
If factors are N x N, then there is a single N x X factor and the standard RNN is recovered.
Thus, there is flexibility between computational budget and statistical performance.
Soft unitary constraint
A regularization term is simply added to the loss :
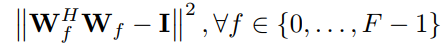
If all the factors are unitary, then the full matrix W is unitary, and if all factors are approximately unitary, then W is also approximately unitary. This new loss term introduces the usual strength hyperparameter like any other regularization term.
Using complex matrices
Imposing a unitary constraint on a real matrix means that the space it can cover is disconnected (because its determinant is either 1 or -1). Using a complex space means that the unitary set is now connected and continuous, and is more easily optimized.
Experiments
NOTE: The authors implemented their own custom CUDA kernels for fast Kronecker operations in C++ (inexistent in Theano, Tensorflow and Pytorch)
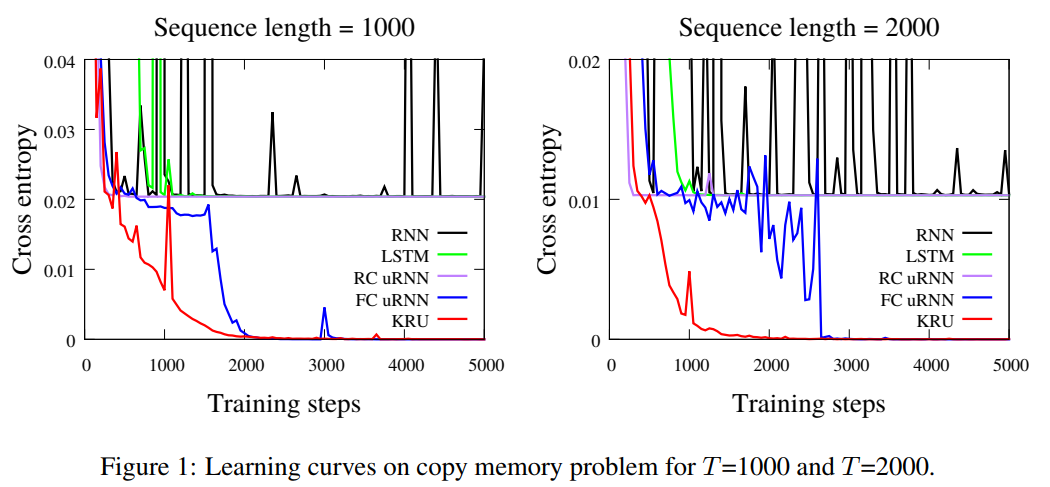
Copy-memory problem (sequence to sequence)
Input : \([x_0, x_1, ..., x_9, \text{blank} \times T-1, \text{delimiter}, \text{blank} \times 10]\)
Target : \([\text{blank} \times T+10, x_0, x_1, ..., x_9]\)
NOTE: Expected cross-entropy for a memory-less strategy is 0.03 for T=1000 and 0.015 for T=2000
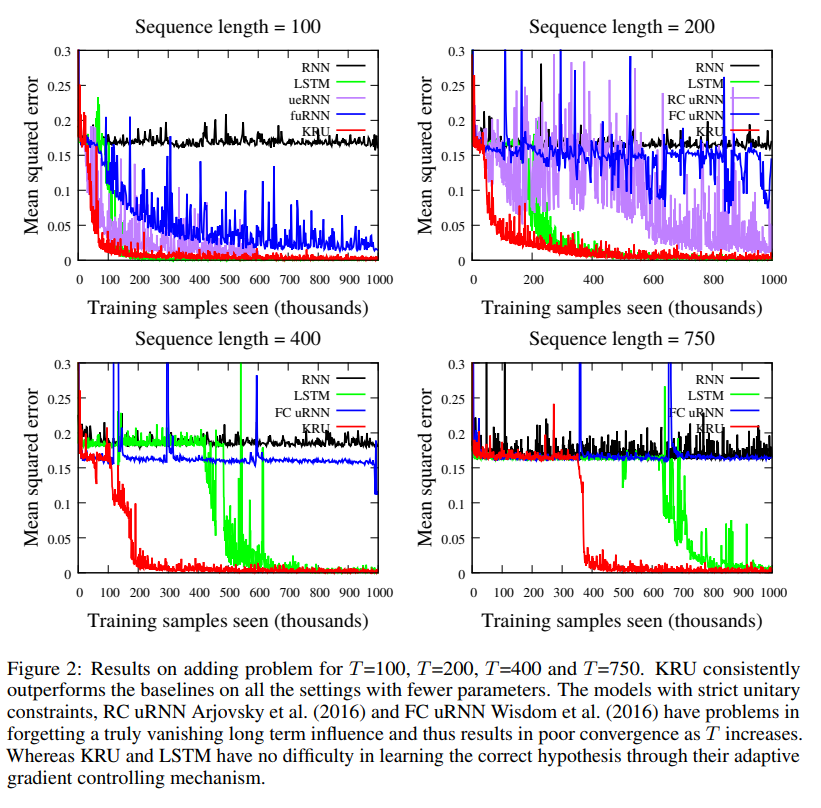
Adding problem
Input : Two sequences (first a sequence of random numbers, then a sequence of equal size, filled with zeros but containing two 1s at random places)
Target : Predict the sum of the numbers in the 1st sequence at the positions defined the ones in the 2nd sequence.
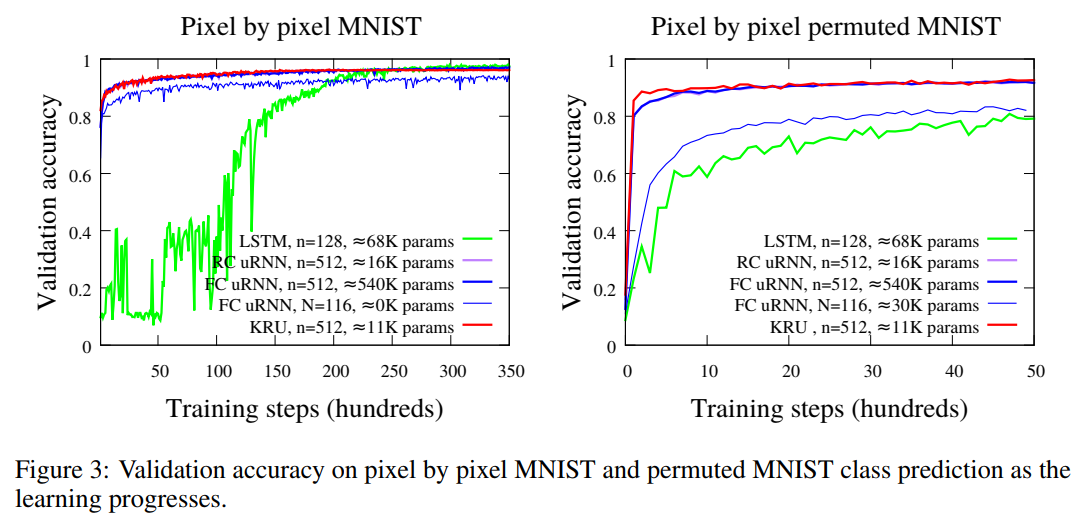
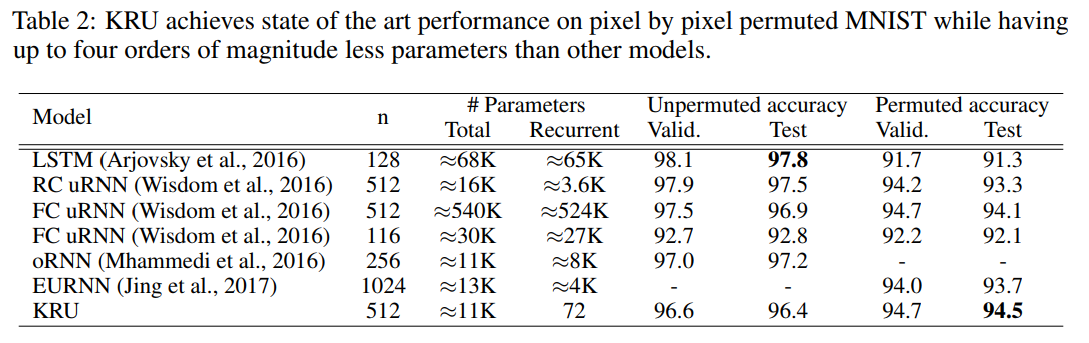
Pixel-by-pixel MNIST classification
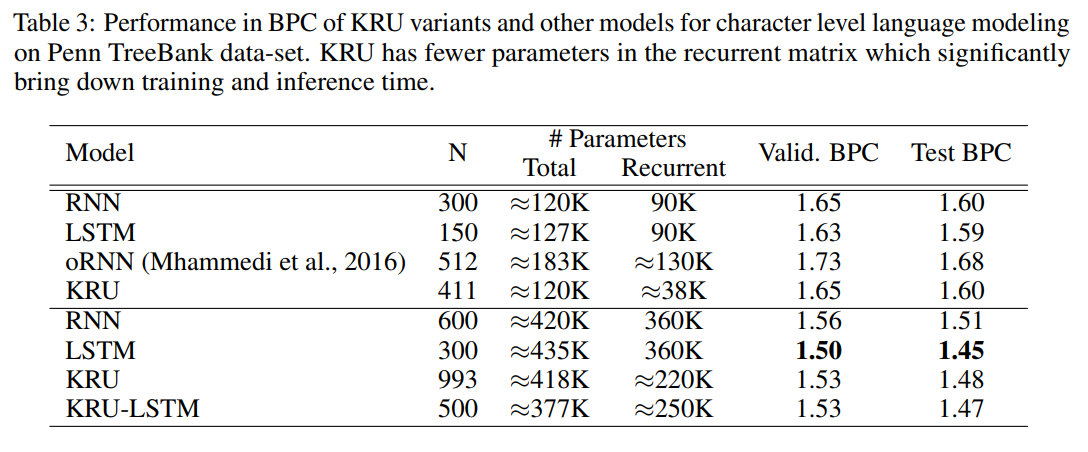
Penn-Treebank character-level modeling
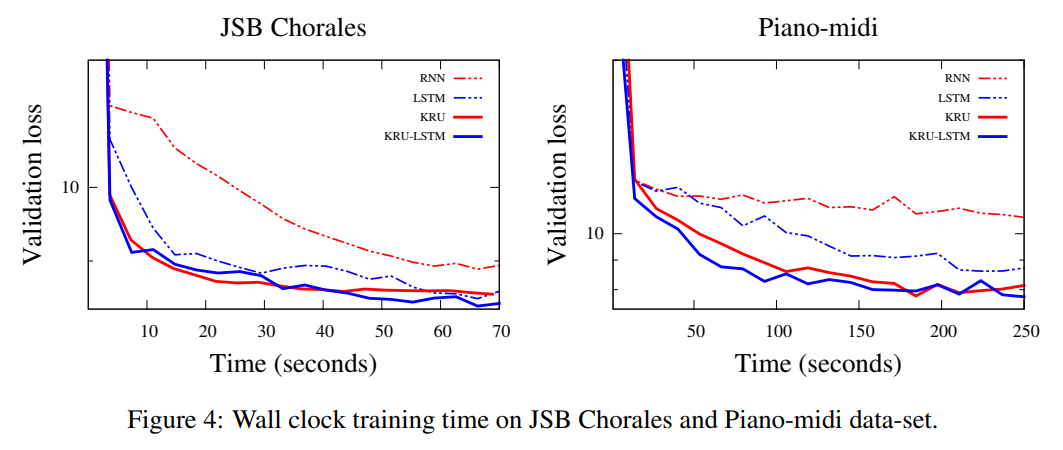
Music modeling