CLIP-Q: Deep Network Compression Learning by In-Parallel Pruning-Quantization
The authors propose a network compression method that combines pruning and quantization.
- They use unstructured pruning, and do not care about acceleration; they only measure the storage requirements of the weight tensors.
- They use a standard sparse coding scheme to acheive practical space savings after quantizing.
- They show strong results.
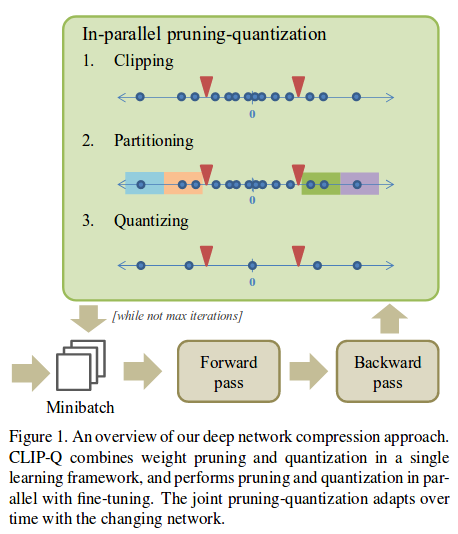
Method

-
Clipping: Set two thresholds \(c^-\) and \(c^+\) so that a fraction \(p\) of all weights are between these thresholds. For the next forward pass, these weights will be set to zero. In the next forward pass, they may be non-zero. \(p\) is constant, but \(c^-\) and \(c^+\) change.
-
Partitionning: Divide the non-clipped portion of the axis of weight values into \(2^b-1\) intervals, where \(b\) is the bits budget.
-
Quantizing: Quantize the weights to the average of their interval (for the next forward pass only).
Setting hyperparameters
Prior to running Clip-Q, we need to find \(p\) and \(b\). The authors use Bayesian optimization; more specifically, they use a Gaussian Process. They use this method for each layer, and find \(\theta_i = (p_i, b_i)\) for each layer \(i\). The optimze the following objective:
\[\mathrm{min}_{\theta} \quad \epsilon(\theta) - \lambda * c_i(\theta)\]where \(\epsilon(\theta)\) is the error on a subset of the training set and \(c_i(\theta)\) is a measure of compression benefit (economy of bits). See section 3.2 of the paper for more details.
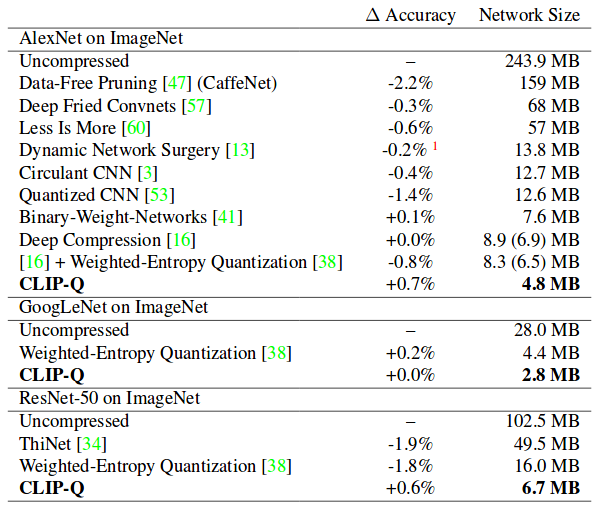
Results