Main idea

Replace the RNN core additive block with a multiplicative block using the Hadamard product.

[Reminder] Hadamard product: \((A \odot B)_{ij} = a_{ij} \times b_{ij}\)

Core block of Vanilla RNN vs Proposed Multiplicative-Integration RNN (MI-RNN):

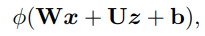\(\rightarrow\)

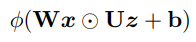
In a more general form, where each matrix has its own bias term:

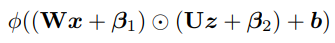
Finally, with an added “gate” on the second order term:

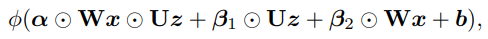
(If \(\alpha = 0\), we get back to the original additive block)

NOTES:

  • Number of parameters is about the same
  • Second-order term shares parameters with first-order terms
  • Can be easily added to existing architectures (e.g. LSTM/GRU)

Gradients

Gradient for vanilla-RNN:

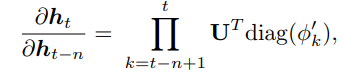
Gradient for MI-RNN:

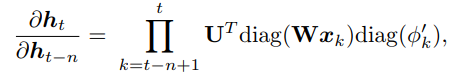
(For the simple case. In the general case, we have: diag\((\alpha \odot W x_k + \beta_1)\))

NOTES:

  • Gradient is now “gated” by \(\text{diag}(Wx_k)\)
  • Gradient propagation is easier with \(Wx_k\) involved

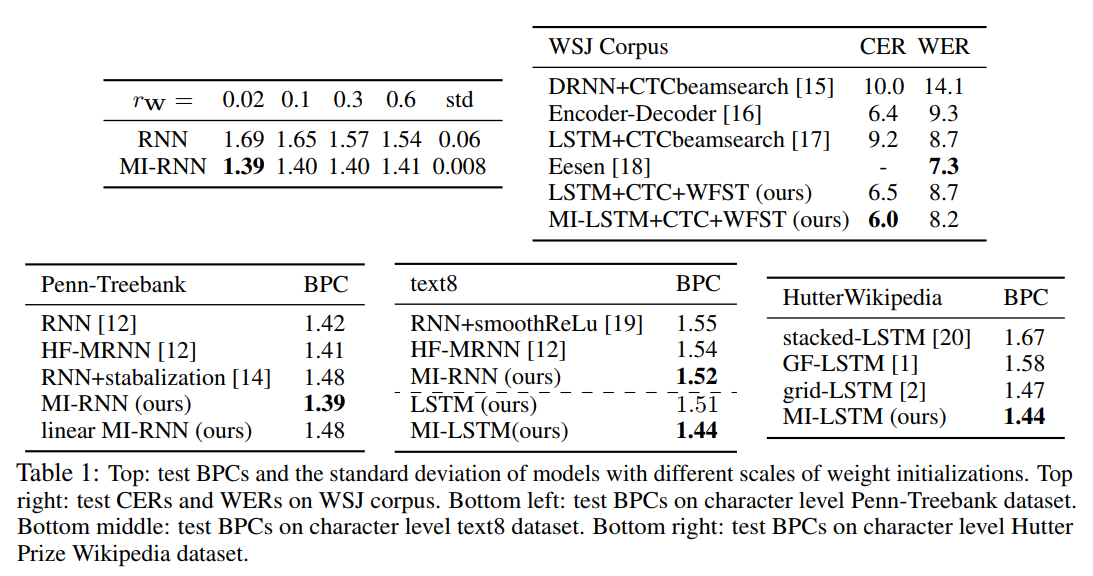
Experiments using Penn-Treebank (text) dataset

Activations problem

Activations over the validation set, using tanh as the nonlinearity

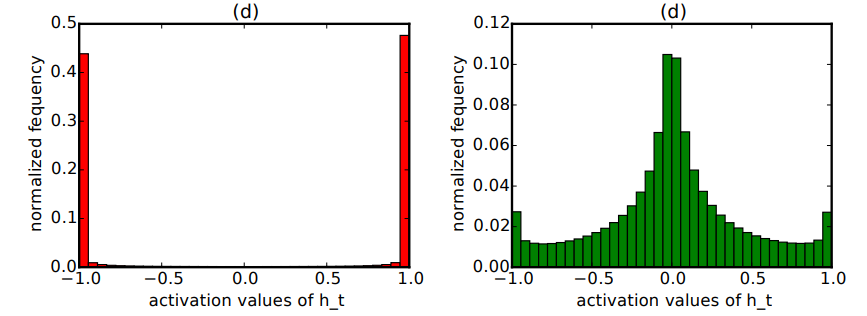
[Reminder] Tanh derivative: \(\nabla \tanh(x) = 1 - \tanh^2(x)\)

  • For saturated activations, \(\text{diag}(\phi'_k) \approx 0\) (no gradient flow)
  • For non-saturated, \(\text{diag}(\phi'_k) \approx 1\)

Scaling problem

  • Pre-activation term : \(Wx_k + Uh_{k-1}\)
  • For one-hot vectors, \(Wx_k\) is much smaller than \(Uh_{k-1}\); initialization matters a lot! (See top-left of Fig.1, where \(r_w\) is the uniform initialization range)

Comparative experiments