Introduction

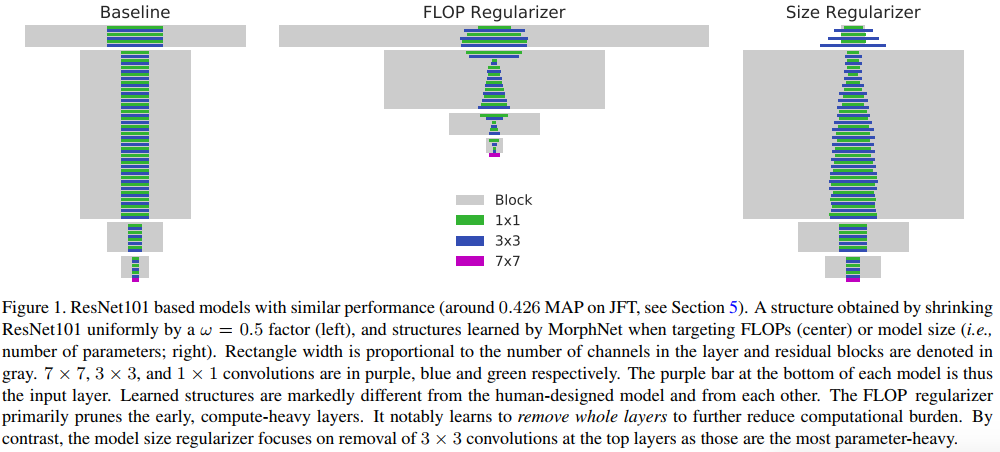
MorphNet is an approach to automate the design of neural network structures. MorphNet iteratively shrinks and expands a network, shrinking via a resource weighted sparsifying regularizer on activations and expanding via a uniform multiplicative factor on all layers. The proposed method has 3 advantages :

  • it is scalable to large models and large datasets;
  • it can optimize a DNN structure targeting a specific resource, such as FLOPs per inference, while allowing the usage of untargeted resources such as model size (number of parameters), to grow;
  • it can learn a structure that improves performance while reducing the targeted resource usage

Method

Let \(O_L\) be the output wight (number of output feature maps) or layer L and \(O_{1:M}\) the total number of feature maps between the first and last layer (M is the index of the last layer). They formalized their problem as follows:

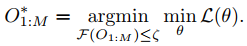
where the goal is to find the most accurate model (with the lowest loss) but which respect a limited resource. For example here, the total number of flops must be below \(\zeta\). They then reformulate the problem as

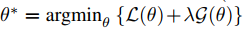
where \(g(\theta)\) is a sparsity regularizer which depends on \(F(O_{1:M} )\). Since their method has no guarantee to satisfy \(F(O_{1:M})\) < \(\zeta\), they proposed Algo 1 where step 1 and 2 are compression steps and step 3 is an expansion step.

The regularizer

The regularizer is given by the following formula:

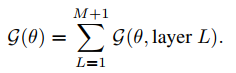
where

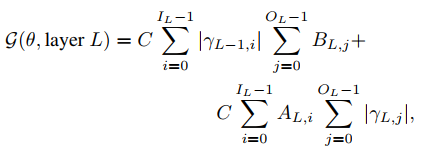
and \(f,g\) is the spatial dimension of the filter at layer L and \(x,z\) the spatial dimension of the feature maps of layer L. Also, \(A_{L,i}\) (\(B_{L,j}\)) is an indicator function which equals one if the i-th input (j-th output) of layer L is alive – not zeroed out.

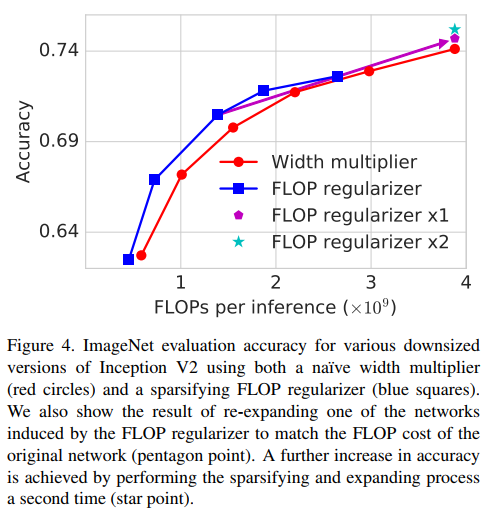
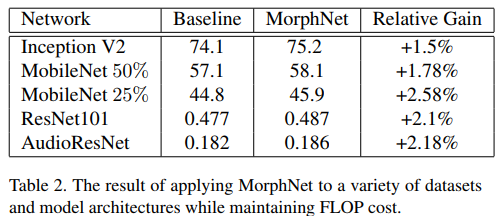
Results

And … the method works!