Neural Processes
In this article, the authors present a new hybrid model between Gaussian Processes and Neural Networks.
Gaussian Processes and Neural Processes
Alternative to NN to perform regression tasks : stochastic process where inference is conditioned on some observations (ex: image pixels). They rely on a Gaussian approximation of parameters distributions.
They can represent as many functions as observations and thus capture uncertainty over predictions. They are fast to train but computationnaly costly at test time, especially with many context points.
Here the idea is to construct a model that :
- learns distributions over functions (GPs)
- can estimate the uncertainty of their predictions (GPs)
- adapts to new context (GPs / NNs)
- is computationally efficient (NN) : scales linearly with the number of context and target points
Neural Processes
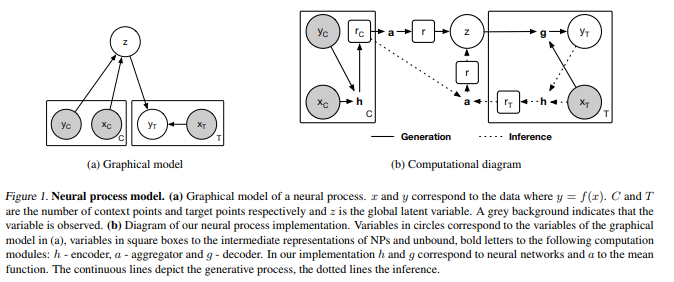
The gist of their intuition (supported by a lot of equations in the paper) is that in order to represent a stochastic process with a NN, one can use the idea of variational auto-encoder (VAE) where a latent representation \(r\) extracted from an encoder \(h\) can contain noise (ex : be a multivariate standard normal).
By using variational inference to learn the decoder \(g\), a family of functions (instead of a single one for neural networks) can be learnt in a single model.
This is done by providing context points whose single aggregated latent representation \(z\) (ex: the mean of latent representations) is also used to generate the prediction on additional target points. Hence, the variable z :
- adapts to the current data
- captures a data-driven prior on the problem
If no contextual point is given at test time, the prior contains prior information on the problem that was learnt at test time.
In meta-learning, this can be seen as a few-shot function estimation.
Experiments on regression
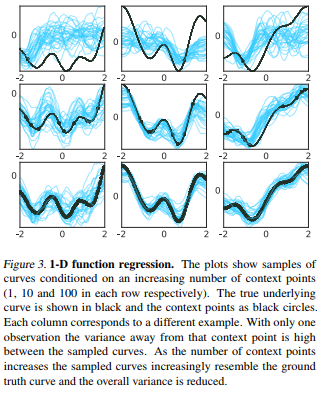
Learning to approximate a 1-D function generated with GPs from a variable number of randomly picked context points:
Learning to approximate a image from a given dataset (MNIST, CelebA) from variable number of randomly picked context points:

Comparing to related methods (Meta-learning, Bayesian methods, Conditional latent variable models…) on a reinforcement learning optimisation task :
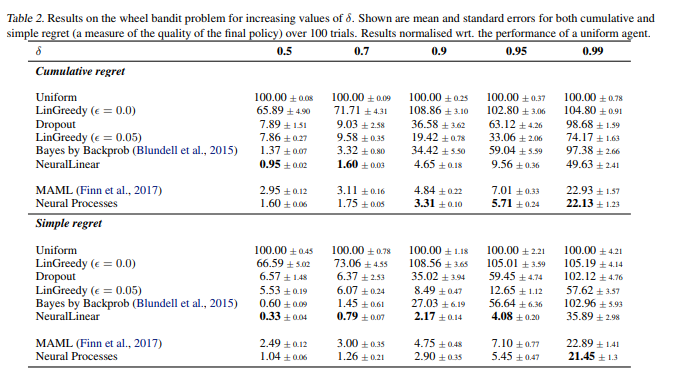
They basically show that their model can be used for various tasks (but mostly show so on low-dimensional regression tasks), is rather competitive compared to SOTA, is fast at test time compared to GPs.