Main Idea

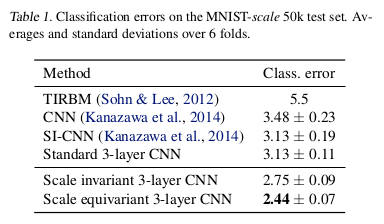
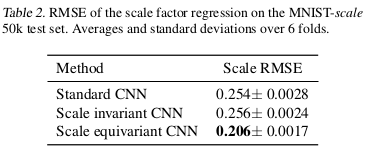
This paper shows the effect of the injection of a local scale equivariance into a CNN. This highlights the usefulness of allowing for a compact representation that can also learn relationships between different local scales by keeping internal scale equivariance.

The three main parts of this work:

  1. A convolutional filter is applied at multiple scales and only information about the maximally activating scale at each location is passed to the output.

  2. The output is composed of the magnitude of the maximally activating scale and of the corresponding scale value itself. These two values are combined into a 2D vector.

  3. Convolutions on this vector field use a similarity metric that takes into account both magnitudes and scale factors.

Scale equivariance

The image name \(x\;\epsilon\;R^{MxN}\).

A representation \(T\) of \(G\) is a function from \(G\) to a family of linear operators such that \(g,h\;\epsilon\;G\): \(T(g)T(h)\;=\;T(gh)\). Where \(g\) is the scaling of the object or pattern and \(T^{\chi}(g)\) to a linear operator that implements this scaling. \(f\) is scale invariant if: \(f(T^{\chi}(g)x)\;=\;f(x)\) and equivariant if: \(f(T^{\chi}(g)x)\;=\;T^{y}(g)f(x)\) where \(y\) is a vector field.

Scale-Equivariant convolution with vector fields

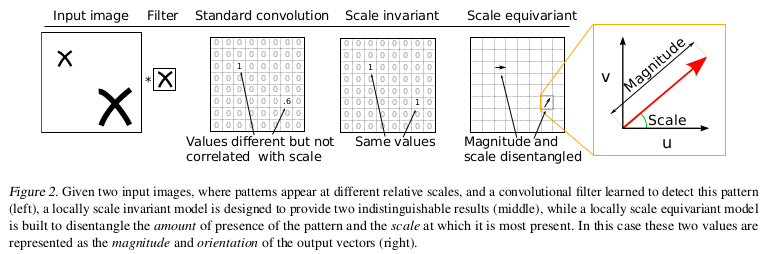
Results