Rotation Equivariant CNNs
Contribution
Observing that regular CNNs exhibit translational invariance but suffer from rotational variance, the authors propose a CNN architecture based on steerable filters (called SFCNN) featuring rotation equivariance. Employing their approach circumvents the need for rotation in data augmentation and reduces the ‘sample complexity’ of the network. The authors’ main argument in support of equivariance properties of a network is that by doing so, the hypothesis space (i.e. the possible transformations found in the data) is reduced which simplifies the learning task.
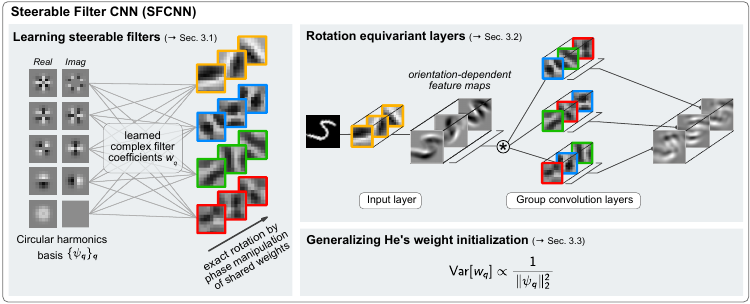
Steerable Filters
-
A filter \(\Psi\) is rotationally steerable if “its rotation by an arbitrary angle \(\theta\) can be expressed” in terms of rotations applied to a set of atomic basis functions \(\{\psi_q\}^Q_{q=1}\) resulting in
\(\rho_\theta\Psi(x) = \sum^Q_{q=1} \kappa_q(\theta)\psi_q(x)\).
-
The authors choose circular harmonics as the atomic basis functions:
\(\psi_q \equiv \psi_{jk} = \tau_j(r) e^{\mathrm{i}k\phi}\).
-
A specific learned filter is obtained by linear combination of these basis functions using weights \(w_{jk} \in \mathcal{C}\) (\(\mathcal{C}\) denotes the set of complex numbers) learned by the network:
\(\tilde{\Psi}(x) = \sum^J_{j=1} \sum^{K_j}_{k=0} w_{jk}\psi_{jk}(x)\).
By choosing the learned weights to be complex, they induce rotations of the basis functions with respect to each other.
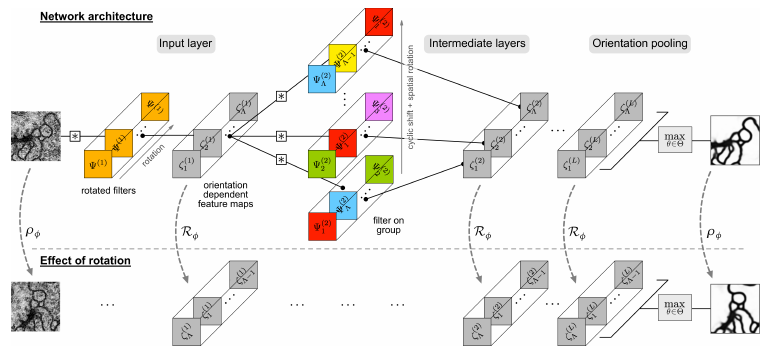
Network architecture
- Output features on intermediate layers are obtained by so-called group convolutions which are a natural extension of spatial convolutions to “general transformation groups”. The group convolution is obtained by “a spatial convolution, rotation and linear combination” (denoted \(\mathcal{R}_\phi\)).
Experiments
Rotated MNIST
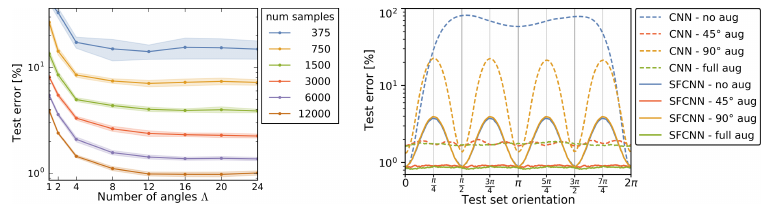
- Left - The test error saturates for more than 12 filter rotations. Also increasing the number of training samples improves performance as expected. The authors point out that an increase from 2 to 4 discrete filter rotations gives the same improvement as doubling the number of training samples. This supports their argument of a limited hypothesis space.
-
Right - Training on conventional MNIST, testing on samples rotated by the particular angle on the horizontal axis. SFCNN with 16 rotation angles.
- a. Even with augmentation the CNNs do not achieve as good performance as SFCNNs.
- b. Augmentation leads to decrease of performance even for testing on unrotated data sets for CNNs, but not for SFCNNs.
- c. SFCNNs exhibit a better “rotational generalisation” than conventional CNNs.
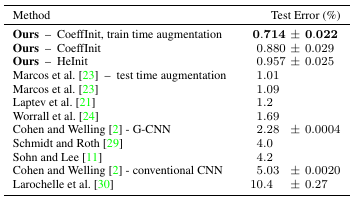
- The method outperforms the state of the art on the rotated MNIST data set. (Note: Especially, the proposed initialisation of the weights has an impact on performance.)
ISBI 2012 2D EM segmentation challenge

- A SFCNN architecture with 17 rotation angles is used to segment images as the one on the left. Training data was augmented (among other transforms) by rotations of \(\frac{\pi}{2}\).
- The author’s submission was rated by the challenge organisers and achieved top 3 performance based on the challenge metrics.