In this paper, the authors describe key ingredients to allow deep neural nets to predict uncertainties. Thereby, they alter existing networks as little as possible to ease adoption and aid practicality. They present two approaches:

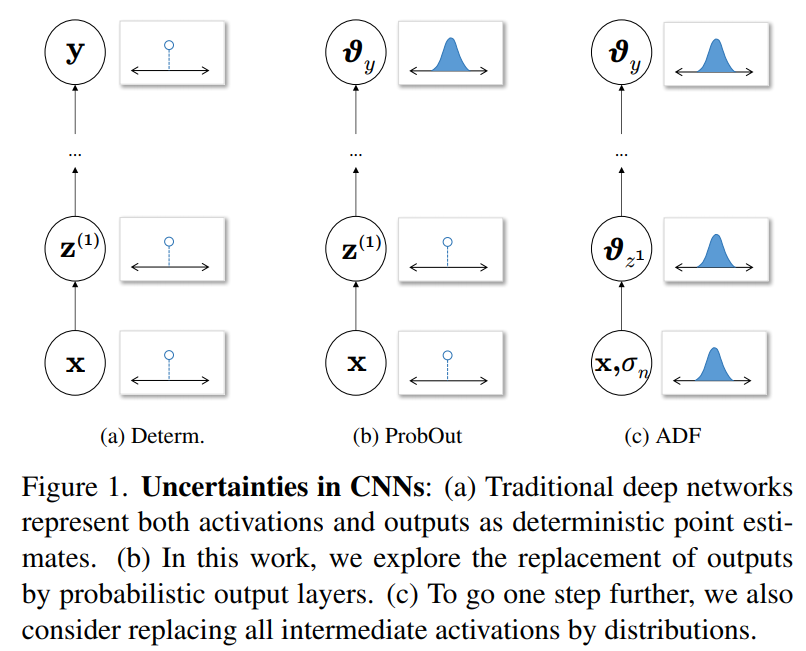
• The first and simplest consists of replacing the output layer of well-proven networks with a probabilistic one (fig.1b).
• The second goes beyond this by considering activation uncertainties also within the network by means of deep uncertainty propagation (fig.1c).

Proposed methods

CNN with probabilistic output

Predictions from standard CNNs can be regarded as point estimates. While this is clearly true for regression networks it is also true for softmax that does not predict how certain the network is in that assessment.

Given the following neural net:

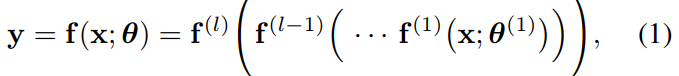
making the output probabilistic would lead to:

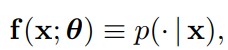
They assume that the output is parametric, and make it Gaussian. A Gaussian output layer, for instance, requires two minimal changes: (i) the number of outputs of the last layer has to be doubled accounting for both mean and variance, and (ii) since variances should be positive, we predict in log space, i.e. \(\theta_y = (\mu, v)\) with \(\sigma = exp(v)\).

Activation uncertainties

Similar to probabilistic outputs, each intermediate layer \(f^{(i)},i=1,...,l-1\) can output a distribution represented by some parameters \(\theta_{z_i}\) rather than a point estimate \(z_i\). C.f. the paper for more detail on how to handle activation functions and backprop.

Results

They show that their method allows to recover the predictions for which the system is not certain (large variance)

A probabilistic neural net is also more robust to adversarial attacks:

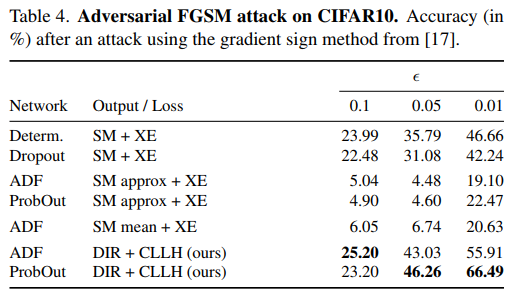
However, although it improves results on CIFAR10 and MNIST, the improvement gap is not very significant