Pose estimation with a Riemannian Geometry loss
In this paper the authors propose to use the geodesic distance of a data-adaptive Riemannian metric as loss function for pose estimation.
The intuition behind it is that the transformation space should not be searched through with separate regressions on rotation and translation parameters because a small change on their values - only slightly penalized by a L2 loss - can actually represent a big error in pose estimation.
First off : Riemannian what ?
A Riemannian manifold is a smooth space equipped with inner products (Riemannian metrics) on the tangent space that vary smoothly from point to point. It has several properties, including that point-wise observations (such as curvature in a compact space) can be extended to local surroundings, which makes it very interesting for shape adaptation problems !
Riemannian Geometry loss
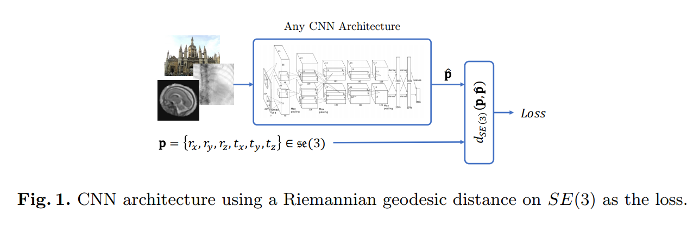
The idea is to use a CNN to predict the best transformation parameters by searching through a solution space that link their optimization, chosen as the tangent space around the identity element of :
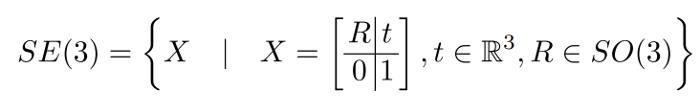
Here is the expression of the Riemannian loss :
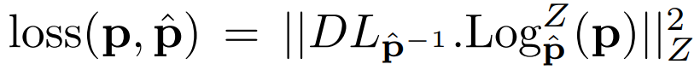
Z being the Riemannian inner product, Log the Riemannian logarithm and L the left translation by \(\hat{p}\) (aka translation in the manifold space).
Interpretation : If Z is the classical canonical (dot) inner product, this loss is similar to a L2 loss on the tangent vector to the manifold in \(\hat{p}\).
Both loss and gradients can be efficiently computed from the jacobian matrix of the inner product.
Experiments
They evaluate their loss function on three applications with GoogLeNet :
- Pose estimation of natural images (PoseNet dataset)
- C-Arm X-Ray to Computed Tomography alignment
- Motion compensation in fetal MRI
They compare to weighted regression on parameters (PoseNet) and anchor points, where the regression is performed on three static points using L2-norm.
Here are the results, with GD the geodesic distance on the manifold :
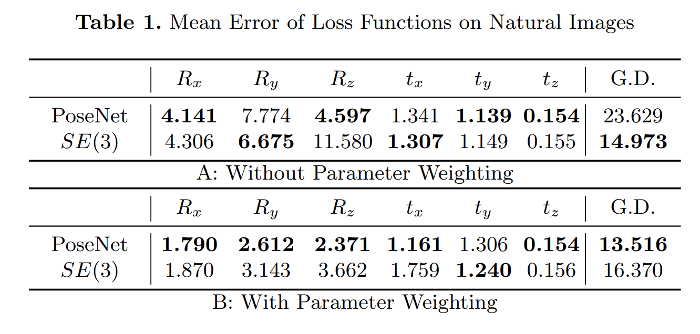
The parameter weights are set to be inversely proportional to the parameters variance on the validation set so that error-prone parameters would be closer to the mean. This gives more accurate prediction results but implies that the parameters no longer follow the manifold, as can be seen on the geodesic distance.
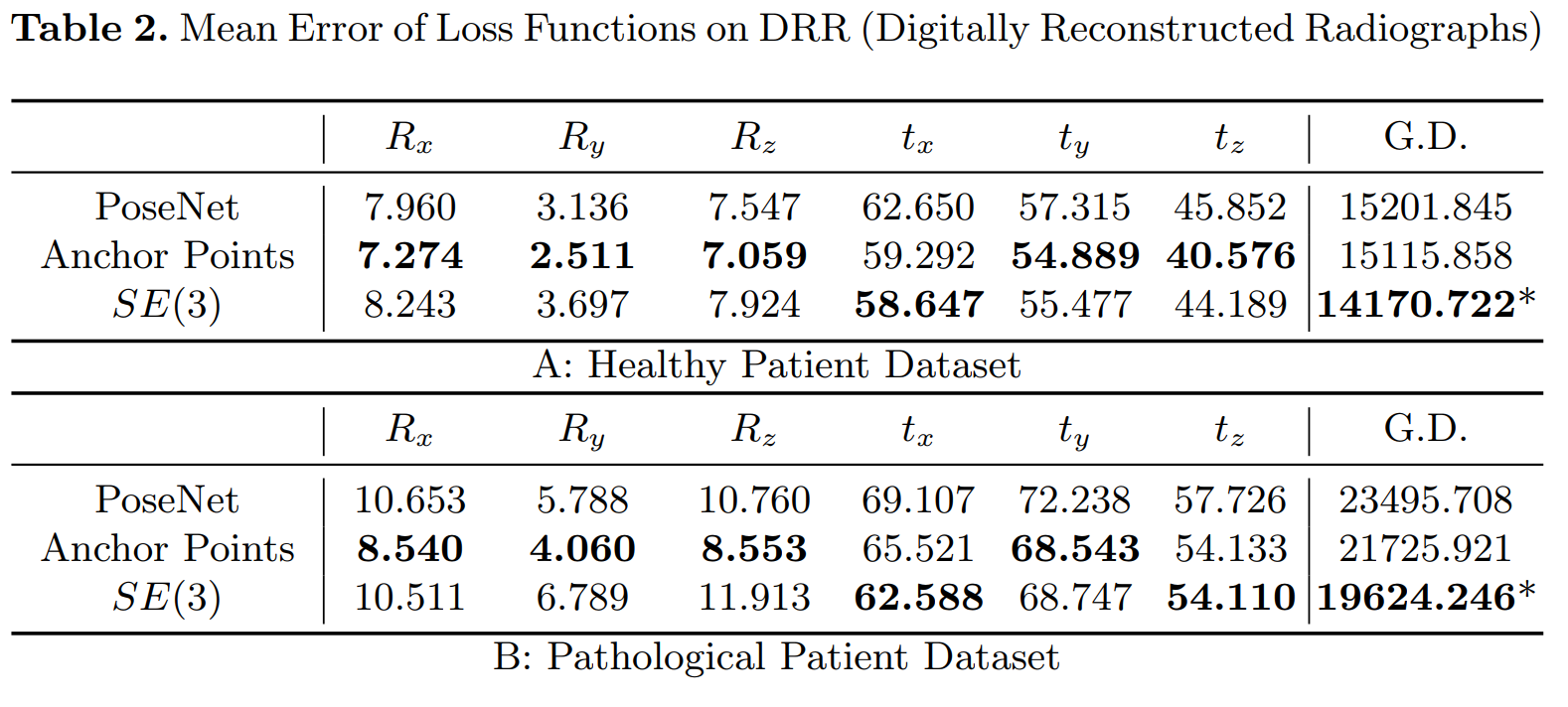
From experiments 1 and 2, it can be observed that without parameters weighting, the new loss allows to obtain a smaller geodesic distance to ground truth values. The authors argue that the grid search is a computationally expensive process when their loss is built automatically from the data.
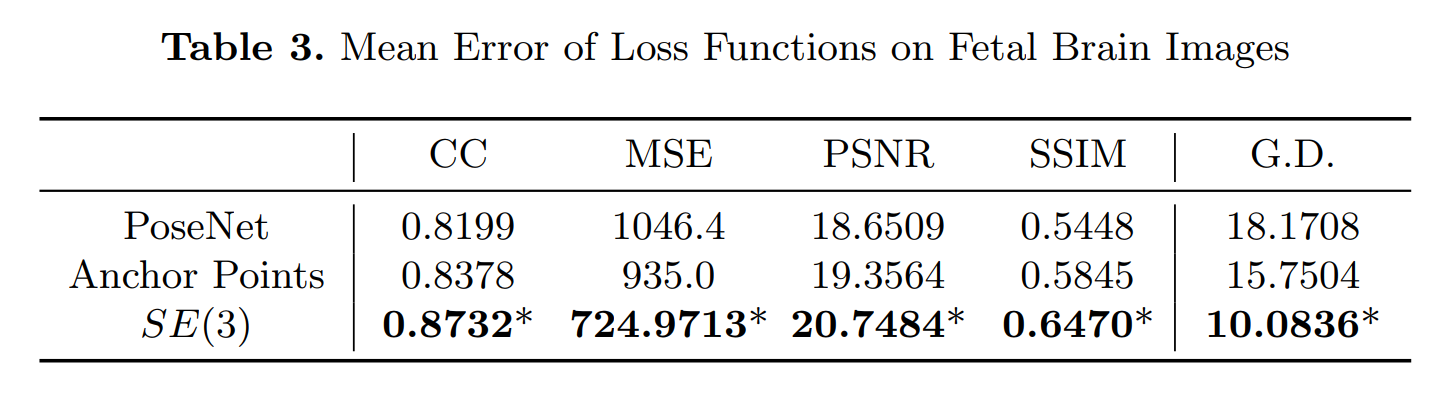
On this dataset, the SE(3) loss function shows drastic improvement in all image similarity metrics, which suggests that a small geodesic distance is linked to a good pose estimation.
Take home message
Metrics, and corresponding training losses, should be adapted to the solution manifold.