The authors propose a method for obtaining resource-efficient neural networks. This method allows to specify a constraint, such as respecting a neuron budget. The method is inspired by the Method of Auxiliary Coordinates (see my other post on that paper).

Neural network pruning as an optimization problem

The authors study 3 pruning costs: C(w) = ||w||_p where p ∈ [0, 1, 2]. These costs are used with 2 different approaches: the constraint form and the penalty form.

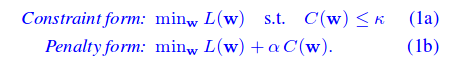
Constraint form

\(w\) are the trainable weights of the network, and \(\theta\) is a set of trainable parameters where each parameter is associated with one in \(w\).

• \(w\) is trained to lower the cross entropy loss
• \(\theta\) is optimized to respect the pruning constraint
• \(w, \theta\) are optimized to be equal

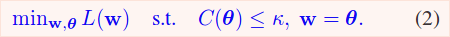
Alterning optimization is used. There is a Learning step and a Compression step. In the learning step, we minimize the following:

\[L(w) + \frac{\mu}{2} |w - \theta|^2\]

We will drive \(\mu \to \infty\). In the compression step, we minimize

||w - \theta||^2 s.t. C(\theta) < \kappa.

In practice, the Compression step is done algorithmically by keeping the top-\(\kappa\) weights in \(\theta\) and zeroing-out the rest (remember that only \(\theta\) is changed here, not \(w\)). See paper for all the crunchy details, formulas, theorems and proofs.

Penalty form

The penalty form is very similar and is proved to be equivalent. The Learning step is the same, and the Compression step replaces the constraint with a term to minimize.

Global vs. Local sparsity

With this method, it is possible to find networks respecting a budget with different compression ratios for each layer, and so naturally.

Results

Results are pretty good

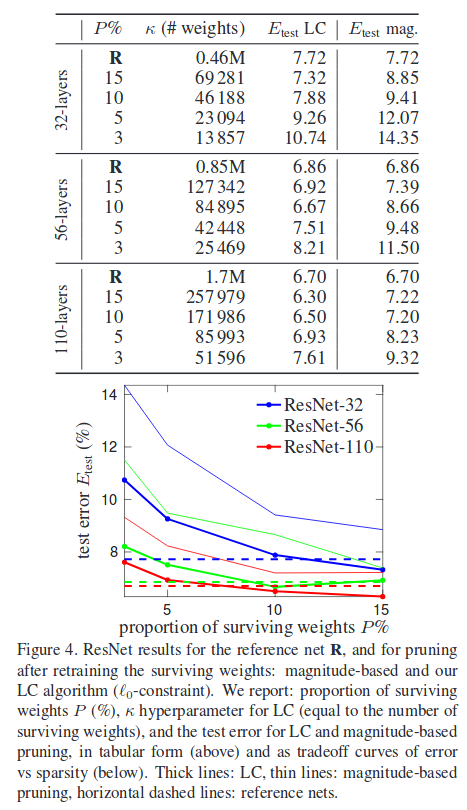
Reproducing the results

Good luck.