Code

Caffe implementation available at https://github.com/hujie-frank/SENet

Contribution

The authors introduce an extension called ‘Squeeze-and-Excitation’ (SE) block which should enable a network “to perform feature recalibration through which it can […] selectively emphasise […] and suppress” features.

They show how such SE-blocks improve performance on several datasets for several architectures while maintaining a reasonable network complexity (in terms of number of parameters as well as computational load).

Proposed mechanism

The basic idea is to enforce the network to regard non-linear interdependencies between spatial features in different channels without any supervised intervention. This is achieved by reducing the output features of a transform block of the original network by a global statistic (e.g. global average pooling) and predicting a scalar weight per channel from such a vector of channel-wise (scalar) statistics.

SE-block

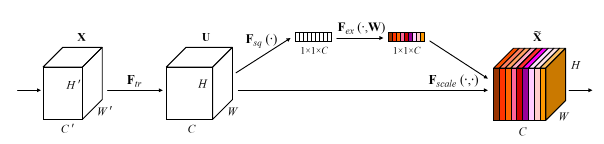
  • \(\mathbf{F}_{tr}\): transform of the original network, e.g. convolutional block
  • \(z_c = \mathbf{F}_{sq}(\mathbf{u}_c) = \frac{1}{H \times W} \sum_{i=1}^H \sum_{j=1}^W \, u_c(i, j)\): squeeze operation
  • \(\mathbf{s} = \mathbf{F}_{ex}(\mathbf{z}, \mathbf{W}) = \sigma(g(\mathbf{z}, \mathbf{W})) = \sigma(\mathbf{W}_2\delta(\mathbf{W}_1\mathbf{z}))\): excitation operation (\(\delta\): ReLU)
  • \(\tilde{\mathbf{x}}_c = \mathbf{F}_{scale}(\mathbf{u}_c, s_c) = s_c \cdot \mathbf{u}_c\): recalibration operation (i.e. rescaling)

Examples for extension of existing architectures

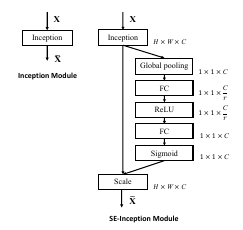
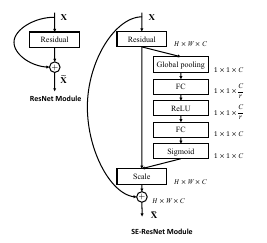
Experiments

Extension of existing architectures

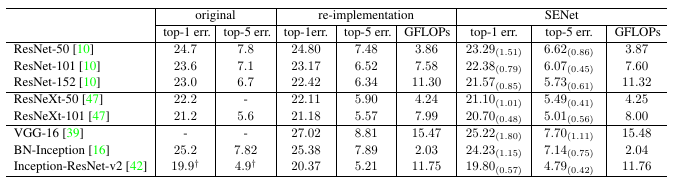
  • SE blocks led to improvements for all investigated base-networks on the ImageNet 2012 dataset.
  • The computational overhead is small.
  • The improvement is the same for different network depths.

Different data sets

  • Similar improvements were also shown for other datasets

    • Scene Classification: Places365
    • Object Detection: COCO

Analysis of reweighting step

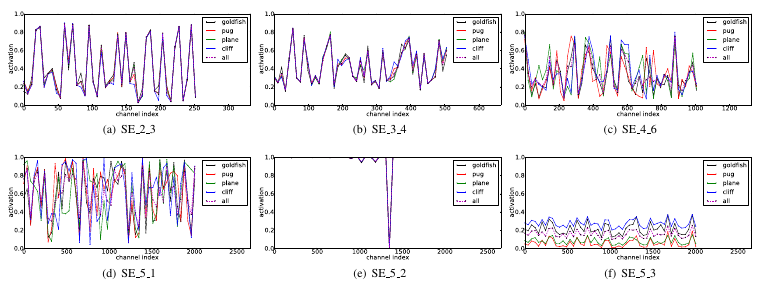
Caption: Colored curves represent the average activations for different classes (computed over 50 samples for each class) plotted over channel index.

  • In ‘early’ layers, the activations of the excitation step (i.e. rescaling weights) are the same among different classes.
  • In ‘later’ layers (e, f), the activations are saturated.
  • The reweighting among channels seems to be most significant in ‘intermediate’ layers.