Goal

The presented approach aims at learning a set of filters for denoising bursts of images taken by hand-held cameras (e.g. in smartphones).

Contributions

  • Synthetic data creation from general purpose images simulating characteristics of real cameras.
  • Pixel-wise 3D kernel prediction for denoising of burst image sequence.
  • Adaptive, weighted (‘annealing’) loss.
  • Generalisation to multiple noise levels.

Conceptual overview

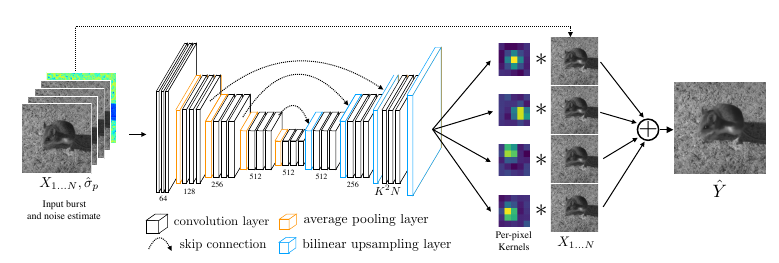
Basic concept

  • input

    • set of series of N images (burst)
    • one image of pixel-wise noise estimates

  • encoder-decoder structure

  • output

    • N filters per pixel in input space (filter size: \(K\) by \(K\))

    • synthesis of output image at pixel \(p\) by

      \[\hat{Y}^p = \frac{1}{N} \sum_{i=1}^N \, <f_i^p, V^p(X_i)>,\]

      where \(f^p_i\) denotes the learned filter at pixel \(p\) in input image \(i\).

Loss

  • main objective

    • \(L^2\)-term on gamma-corrected images

    • \(L^1\)-term on gradients of gamma-corrected images

      \[\ell(\hat{Y}, Y^\ast) = \lambda_2 \, \left\lVert\Gamma(\hat{Y}) - \Gamma(Y^\ast)\right\rVert_2^2 + \lambda_1 \, \left\lVert\nabla\Gamma(\hat{Y}) - \nabla\Gamma(Y^\ast)\right\rVert_1^2\]

  • annealed loss (This is the actual loss term!)

    • time dependent individual image loss term

    • idea: steer training in the beginning to avoid convergence to local minima

      \[\mathcal{L}(X; Y^\ast, t) = \ell\left(\frac{1}{N}\sum_{i=1}^N \, f_i(X_i), Y^\ast\right) + \beta\alpha^t \sum_{i=1}^N \, \ell(f_i(X_i), Y^\ast)\]

Synthetic data creation

  • The authors develop an approach to model several artifacts involved in creation of raw data from real camera sensors, including e.g.

    • explicit model for signal noise

    • simulated misalignment due to sensor movement

Experiments

Settings

  • filter size: K = 5
  • number of input images: N = 8

Nomenclature (KPN methods)

  • 1-frame: N = 1
  • no ann: basic loss function only (@see main objective)
  • sigma blind: no noise estimate as input
  • direct: directly synthesise output pixel values (by adding three additional conv layers)

Synthetic data set

  • KPN always outperforms state of the art

  • multi-frame info, annealing loss and noise estimate are all helpful

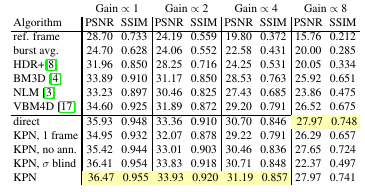
Real data set

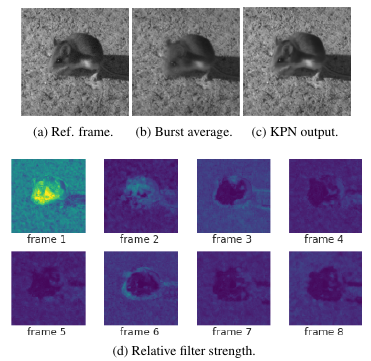
Predicted kernels

  • The approach is robust to object movement (the mouse).

  • The authors claim that their ‘annealing’ approach helps focusing on a single frame where movement occurs, while taking advantage of all frames in static parts of the image (i.e. background).

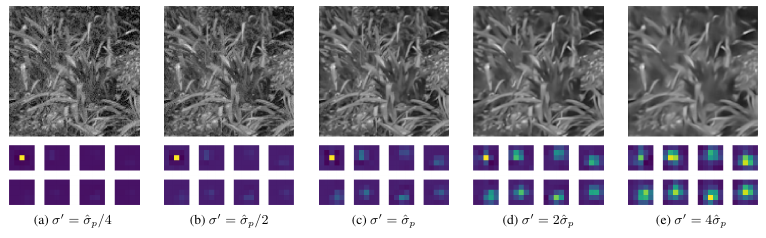
Adaptation to noise levels

  • Noise estimation

    • did not improve training loss
    • but helps for generalisation to larger (unseen) noise levels

  • Learned filters adapt to the noise estimate in the input

    • (a) to (e): scalar multiples of noise estimate for same image burst