Introduction

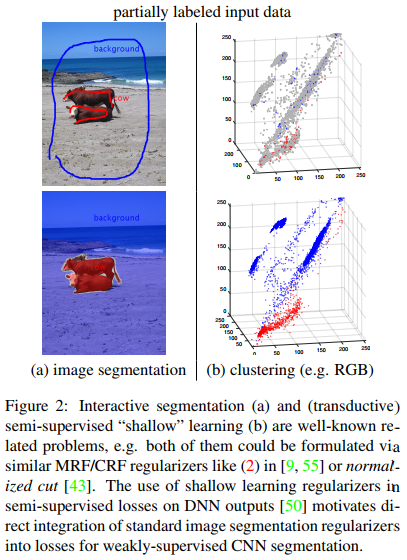
They proposed a weakly-supervised approach to generate full masks from partial inputs (e.g. scribbles or seeds) using standard interactive segmentation methods as preprocessing. To ensure a more accurate result, they propose a new loss function inspired by a well-known criteria used in unsupervised segmentation, e.g. normalized cut.

Method

Normalized cut is a method that comes from the spectral clustering theory. In short, for a 2-class segmentation problem, given a graph \(\Omega\), it looks for two complementary subgraphs \(\Omega_k\) and \(\Omega/\Omega_k\) that would minimizes the following loss:

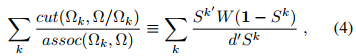
Where \(cut\) is the cost of cutting the graph in two and \(assoc\) is the size of the two subgraphs. This energy term can be reformulated as the element on the right hand side of (4), i.e. \(S^k\) a binary indicator vector for subgraph \(\Omega_k\), \(W\) is a nb_pixels x nb_pixels similarity matrix, \(d\) is a degree vector : \(d_i =\sum_j W_{ij}\).

Since the minimization of (4) is NP-Hard, as usual \(S^k\) is replaced by a soft vector with values between 0 and 1.

The proposed loss is the sum of a usual cross-entropy and a normalized cut term:

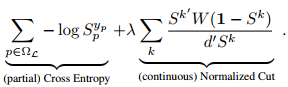
They also show that this Normalized cut is differentiable and thus end-to-end trainable.

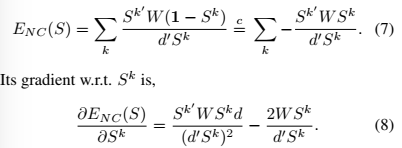
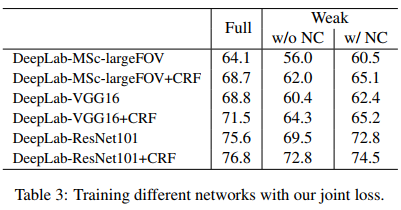
Results

Results of their method are close to that obtained with full supervision