The authors introduce the Method of Auxiliary Coordinates (MAC), a method for training nested systems such as deep neural networks. With this method, layers are trained independently, with a coordination constraint. Like with Expectation-Maximization, there is two alternating steps:

• M step: minimize (train) layers
• C step: coordinate layers

This method can replace backpropagation. It has many advantages:

• Can work with nondifferentiable or discrete layers
• Embarrassingly parallel
• Proven to converge
• Reuses existing algorithms from shallow models

Formulation

Here, we will compare formulations in a regression setting, but we could also do it for classification.

The Nested Objective Function

We can write the usual nested training approach as follows:

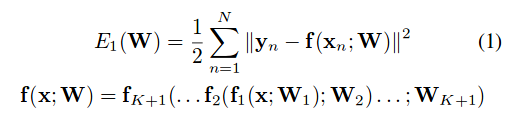
The way we solve this problem is using backpropagation.

The MAC

An auxiliary variable z is introduced per data point and per hidden unit.

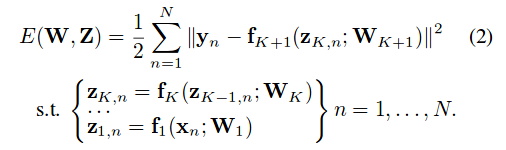
We optimize the output of the system to match the target value y, subject to the constraint that each auxiliary variable match the output of the preceding layer. One way to solve this constrained optimization problem is using Quadratic-Penalty Optimization:

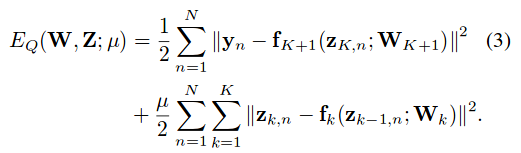
The Alternating Direction Method of Multipliers (ADMM) can also be used and is expected to perform better by the authors.

Architecture search

MAC is well adapted for model selection. For neural networks, model selection is a discrete optimization problem where we optimize the number of neurons in each layer. MAC has inspired the paper “Learning-Compression” Algorithms for Neural Net Pruning, also from Miguel Carreira-Perpinan. In this paper, the architecture is a set of auxiliary variables, a kind of mask that is constrained to respect a budget. The layer weights independently learn to accomplish the task but are constrained to respect the mask. (Review of this paper available soon.)