Budgeted Super Networks
The authors propose to use a Reinforcement Learning scheme to find the most efficient architecture among a set of possible layer combinations that should optimize a cost constraint (computation, memory consumption, distribution ability).
Super Networks
First, the authors present two “Super Network” architectures, that represent the space in which the optimal solution is sought.
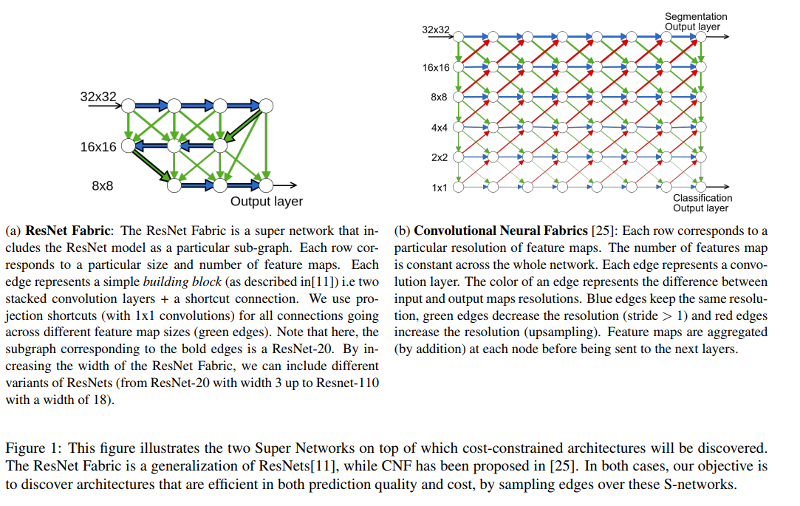
Any architecture of their scope can be seen as the result of an Hadamard product between the direct acyclic graph (DAG) of the Super Network and a binary matrix H that encodes which connections are kept and which are deactivated.
They derive a stochastic model of Super Networks that allows the search process to take place in two steps :
-
Sample H from a distribution T
-
Use the corresponding network to make a prediction
-
Optimize both sampling distribution and network parameters with a policy-gradient based algorithm.
Any measurable at training time cost could be used. The proof that this leads to an optimal solution is given in Supplementary Materials and the code is publicly available.
Experiments
They apply this model on : CIFAR 10/100 : classification Part label : segmentation
The authors propose to either optimize the number of operations, the number of parameters, or the distributive potential.
Here are some architectures found as optimal :

On all applications, they show that they can either obtain the same performance as the State-of-the-Art with a lower cost architecture (ex: a network that contains 4 times less parameters) or outperform it with a slightly bigger budget.