In this paper, the authors propose a novel metric to describe the difficulty of solving a task for a family of networks architectures on a given dataset. This metric is called Intrinsic Dimension. For example, the intrinsic dimension of classifying MNIST digits using a MLP is 750. Adding more layers or widening the network does not change this metric.

This metric is obtained by optimizing network parameters along random subspaces, and finding the minimum dimension of a subspace that solves the task.

Subspace optimization

Typically, when optimizing a MLP with a parameter vector \(\theta^{(D)}\) of size \(D\), we take steps on the full “native space” \(\theta^{(D)}\). In “subspace optimization”, we sample \(d\) < \(D\) random directions in \(\mathbb{R}^D\), and we optimize in the subspace \(\theta^{(d)}\). Thus, we need a mapping from \(\theta^{(d)}\) to \(\theta^{(D)}\):

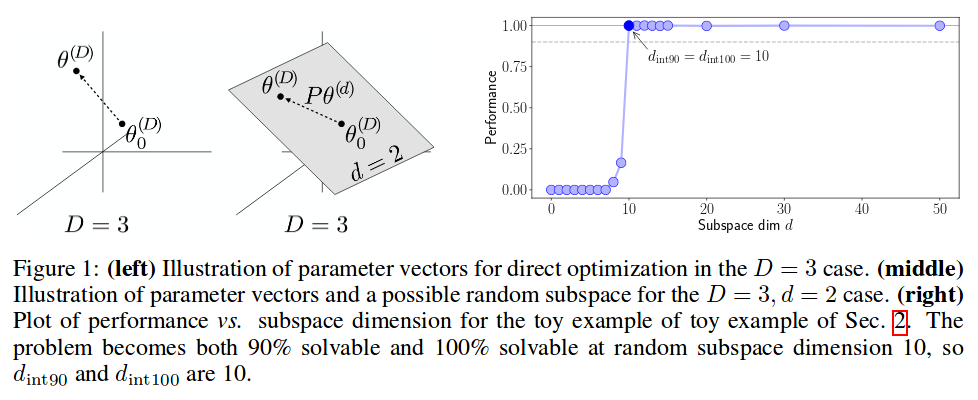
\[\theta^{(D)} = \theta^{(D)}_0 + P\theta^{(d)}\]

where \(P\) is a \(D \times d\) projection matrix, and \(\theta^{(D)}_0\) is the initialization of the parameters. Below is a visual example for a two-layer MLP:

Please take a moment to notice that we typically don’t have \(\theta^{(d)}\) and \(P\), and we take steps on \(\theta^{(D)}\). However, here, we take steps on \(\theta^{(d)}\). Also note that \(P\) is not trainable; it is determined at the beginning of training.

Measuring the Intrinsic Dimension

Take a specific model architecture
Take a subspace dimension \(d\) and sample many subspaces in it
Construct \(P\) for each of these subspaces
Repeat steps 2 and 3 for many \(d\)
For each different \(P\), train the model using this subspace
Plot a graph like Figure 1 (right) to determine the minimal \(d\) where the task is considered solved.

\(d_{int100}\) (“int” for intrinsic) is the \(d\) for which the authors obtain the same performance as using the full native space. \(d_{int90}\) is the \(d\) for which the authors obtain 90% of the performance. For their experiments, they use \(d_{int90}\) as the intrinsic dimension. See paper for a justification.

Experimental results

Task	Model	Intrinsic Dimension	Notes
MNIST	MLP (D = 200,000)	750	Much less than single layer linear (7840) and less than size of input (784).
MNIST	MLP (same but wider)	750	Width does not change Intrinsic Dimension
MNIST	MLP (same but deeper)	750	Depth does not change Intrinsic Dimension
MNIST	CNN	290	The task is easier using spatial information
CIFAR-10	MLP	9000
CIFAR-10	CNN	2900	Interpretation: 10 times is difficult as MNIST