deep-learningCNN

Deep Complex Networks

Reviewed on May 11, 2018 by Pierre-Marc Jodoin • https://openreview.net/pdf?id=H1T2hmZAb

Reference : C Trabelsi, O Bilaniuk, Y Zhang, D Serdyuk, S Subramanian, J F Santos, S Mehri, N Rostamzadeh, Y Bengio, C J Pal. Network compression and speedup. ICLR 2018.

Introduction

In this paper, they show how to use complex numbers (\(a+bi\) where \(i=\sqrt{-1}\)) in a deep neural network.

There are two main motivations to this work

Complex numbers, are numerically efficient and stable in the context of information retrieval from an associative memory
Using complex weights in neural networks also has biological motivation. The complex-valued formulation allows one to express the neuron’s output in terms of its firing rate and the relative timing of its activity. The amplitude of the complex neuron represents the former and its phase the latter

The main contributions of this paper are:

New complex conv operation
New ReLu-based activation functions
New complex batch norm operation
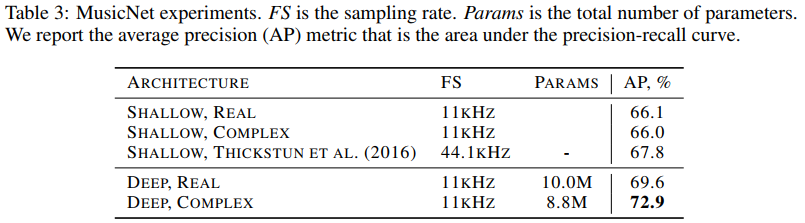
A state of the art result on the MusicNet multi-instrument music transcription dataset,
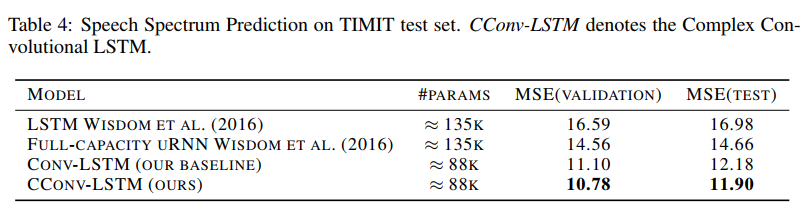
A state of the art result in the Speech Spectrum Prediction task on the TIMIT dataset,

The main drawbacks of complex nets are:

complex multiplication is 4 times more expensive than its real counterpart
the real-valued model performs better in terms of accuracy for the image classification task

How it works

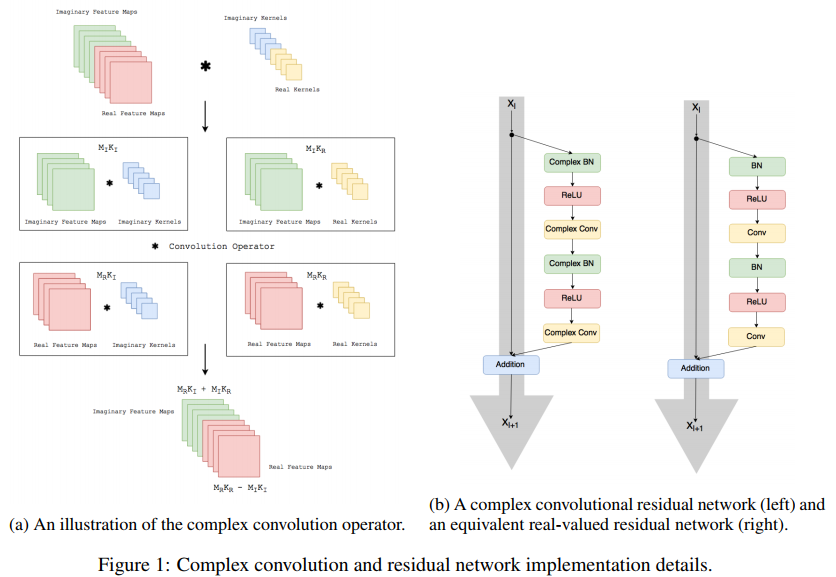
The convolution is made like this

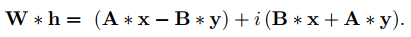
where the first feature maps are the real values and the last are the complex values. They also propose two complex relu functions i.e.

.

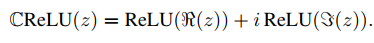
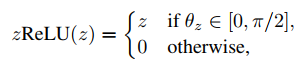
And finally, they propose a new batch normalization

. .

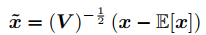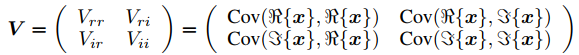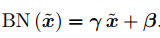
All of this is summarized here :

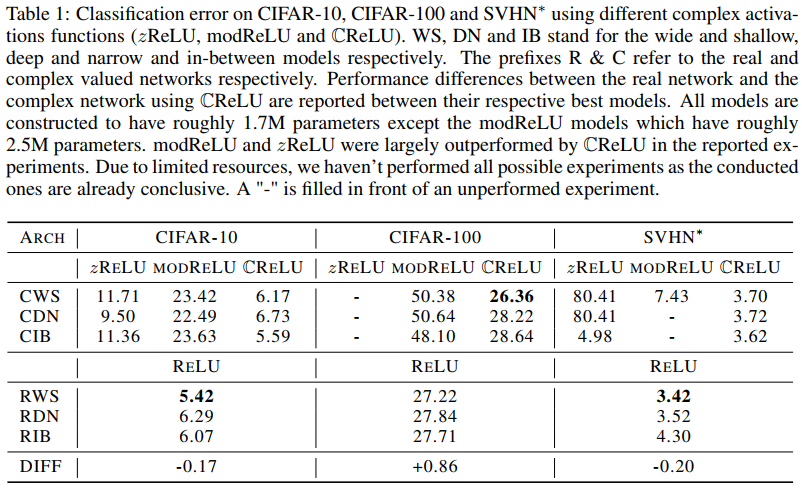
Results

In short : it doesn’t work for image classification but does work for music and speech analysis.

Code

Code can be found HERE