Learning Sparse Structured Ensembles with SG-MCMC and Network Pruning
Description
In this work, learning a Sparse Structure Ensemble within a single training process by Bayesian posterior sampling on model parameters is proposed in two phase to acheive a high prediction accuracy and reduce memory and computation cost. The authors, in the first phase, run an SG-MCMC to draw an ensemble of samples from the posterior distribution of network parameters. In the second phase, weight-pruning is applied to each sampled networks and then retraining over the remained connections. For each test point $hat{x}$, predictive distribution is:
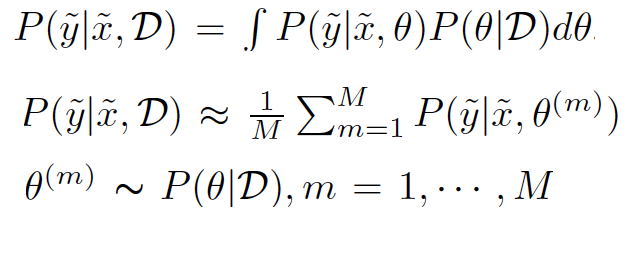
The parameters are approximated by Mont Carlo which will be sampled from posterior distribution of network parameters.
(SG-MCMC) sampling:
MCMC is a common sampling but is not good for large datasets. Stochastic Gradient Markov Chain Monte Carlo (SG-MCMC) represents a family of MCMC sampling algorithms which handling large datasets efficiently and works by adding a scaled gradient noise based on minibatchs and thus improve exploration of the model parameter space. $U$ is known as the potential energy and $hat{U}$ is its approximation over t-th mini bach and (\epsilon) is learning rate.
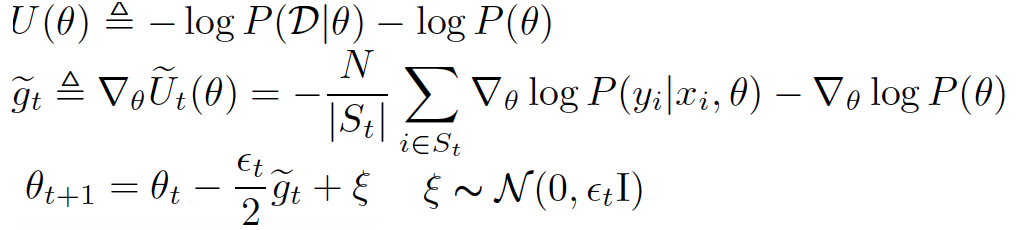
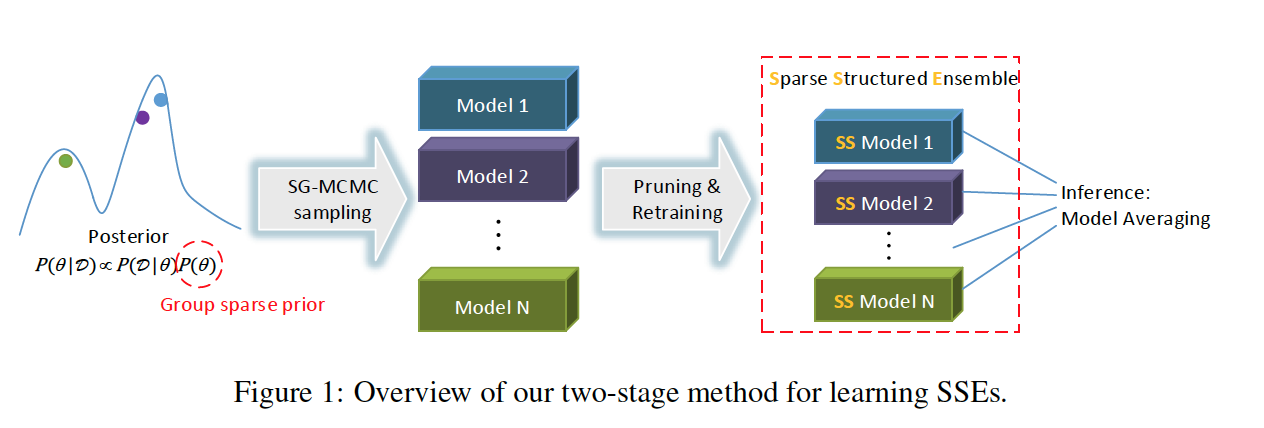
After all the models are collected, authors use a simple pruning rule to reduce the model size as well as the computation cost with finding the network connections whose weights are below a certain threshold and removing them away. Now coming to next phase, with multiple sparse models, there is zero positions in weight matrics is an issue, so authors use Sparse Structure Ensemble (SSE) which employe group lasso regularization, proposes to do feature selection in group level, which means keeping or removing all the parameters in a group simultaneously to achieve structured sparsity corresponding to grouping strategy and penalize unimportant filter and channels. So, group lasso regularization can be formulated as :
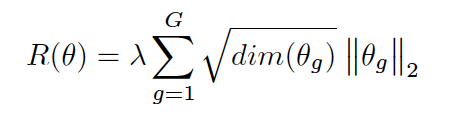
where $\theta$ is a group of weights, G is the number of groups, dim($\theta$) is number of weights.

The SSE is learned on both Fully Neural Network and LSTM. So, the group for FNN is all the outgoing connections from a single neuron (input or hidden) together, it means if neuron’s outputs are all zeros, it makes no contribution to the next layer and can be removed which reduces the rows and columns of weight matrices between layers. In Lstm, Since the input and hidden units are used four times, keeping two index lists during pruning to record the remained rows and columns for each weight matrix. When doing computations, just using partial units to update partial dimensions of the gates according to the index lists. The first grouping strategy is to group each row and each column for the four weight matrices separately (is named untied) and the second is getting a W matrix which concatenated horizontally of four weight and group each row and column of W as a second grouping (tied) strategy and uses two indexes instead four indexes. The other strategy would be Intrinsic Sparse Structures (ISS), is proposed to reduce the hidden size by grouping all the weights associated with a certain hidden unit together and removing them simultaneously.
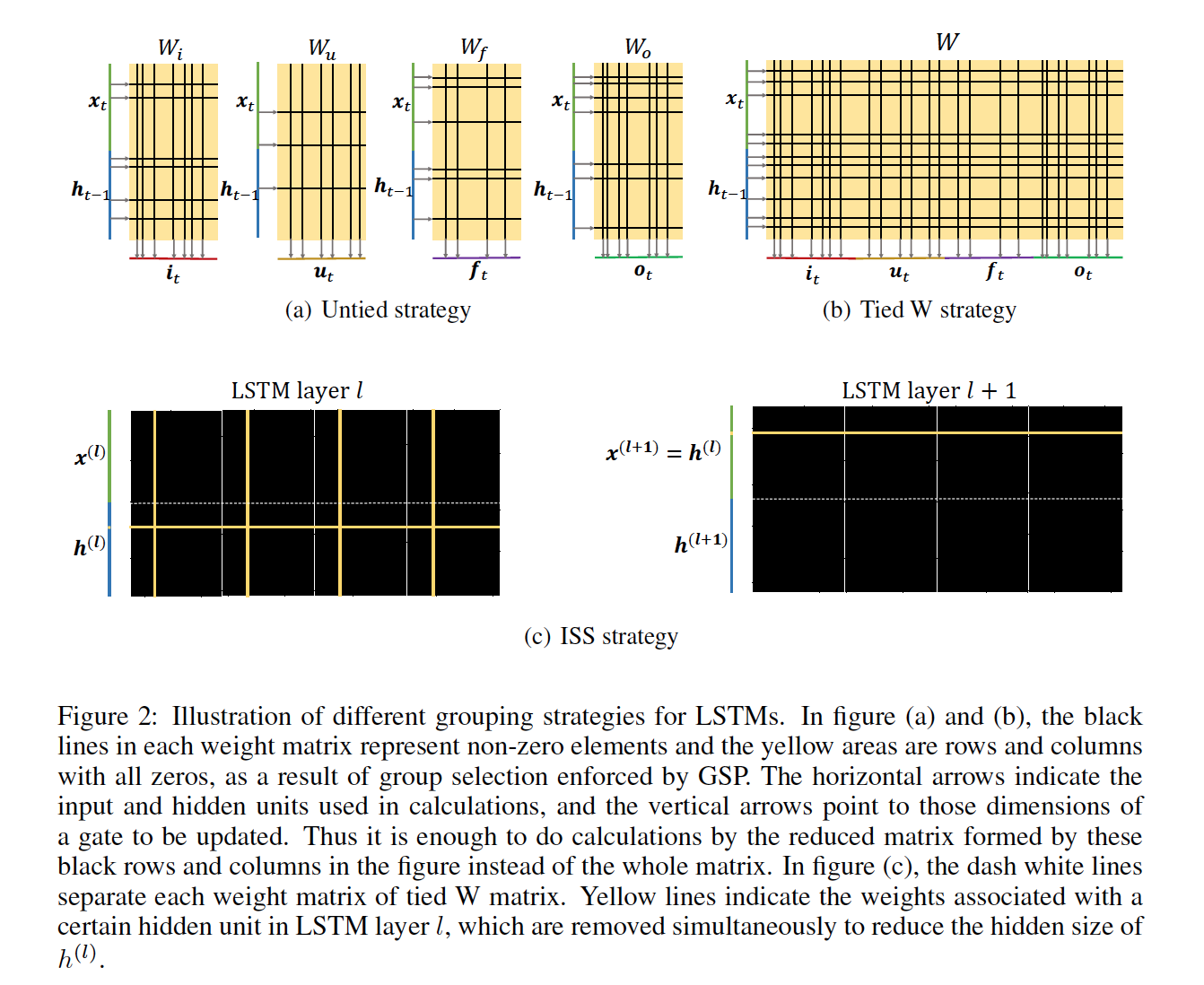

Experiments
The result is shown in two parts: SSE of FNNs for image classification task on MNIST and learn SSE of LSTM models, language modeling task on Penn TreeBank corpus.
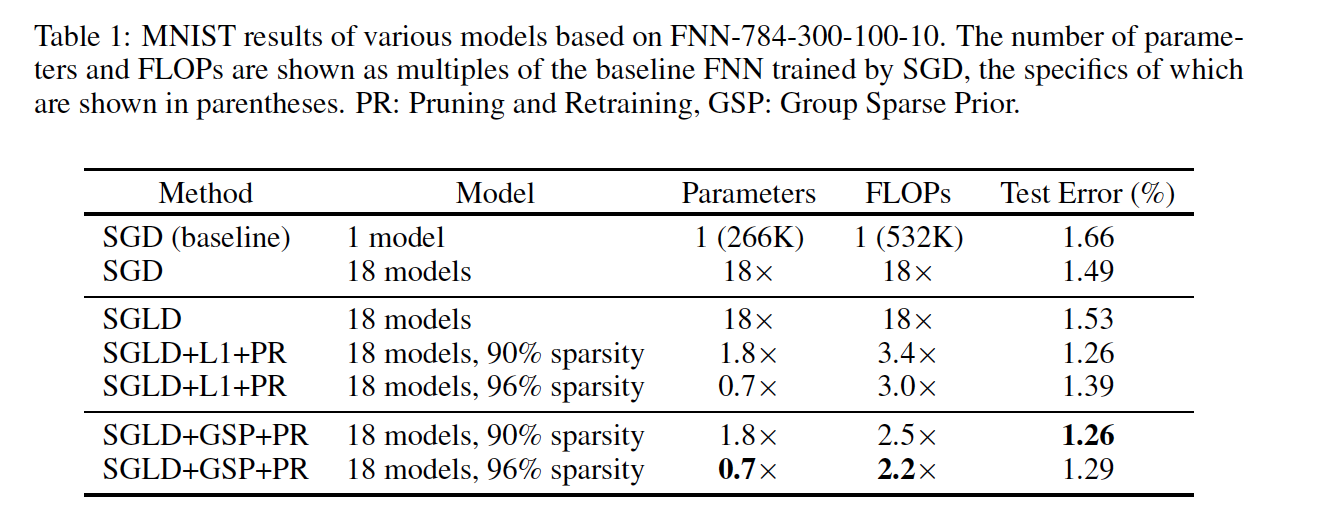
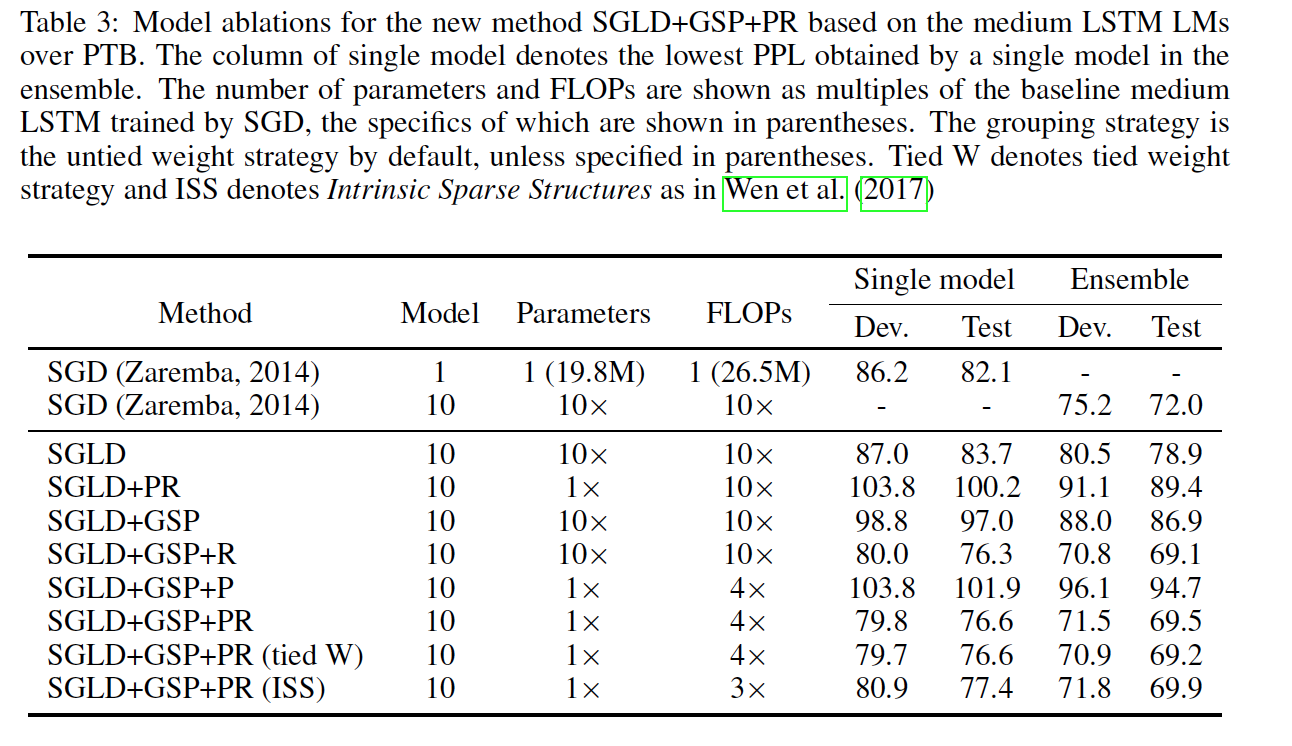
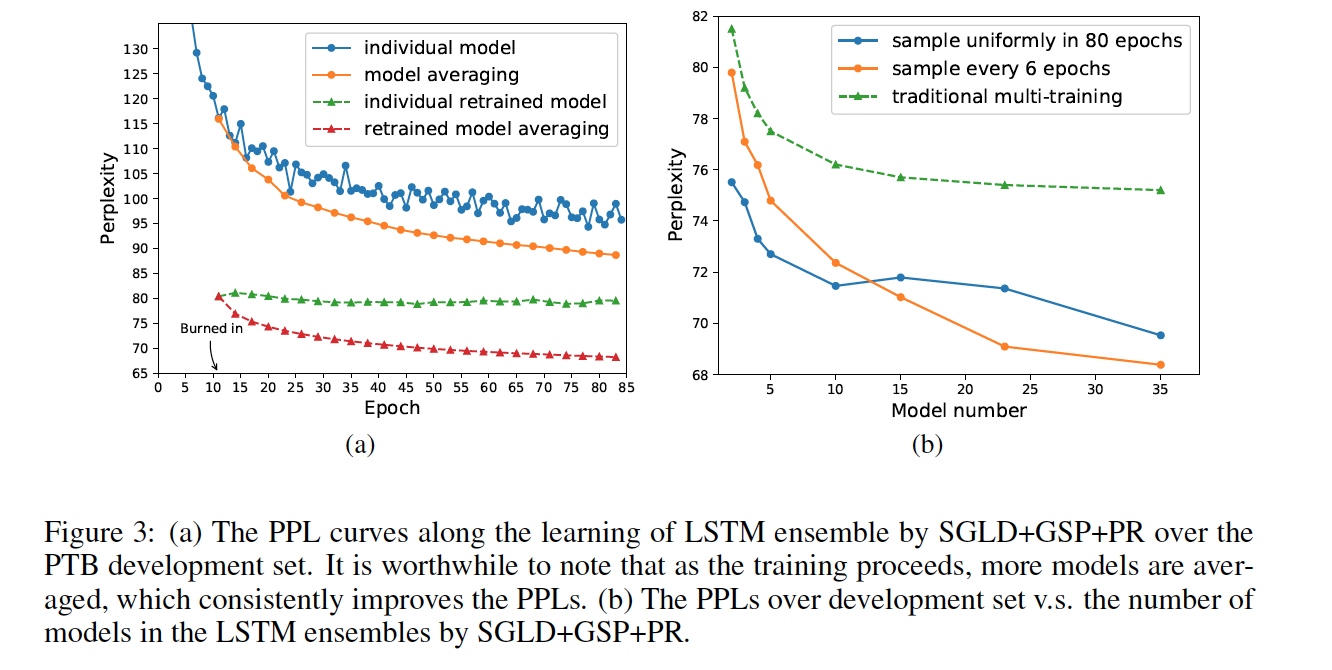
Recall from Wikipedia :
The normal regularization penalizes each weight component independently, which means that the algorithm will suppress input variables independently from each other. In several situations, we may want to impose more structure in the regularization process, so that, for example, input variables are suppressed according to predefined groups. Structured sparsity regularization methods allow imposing such structure by adding structure to the norms defining the regularization term.