The authors propose to describe datasets with topology, a mathematical field whose purpose is to characterize data.. Using this technique, they propose a data-first architecture selection.

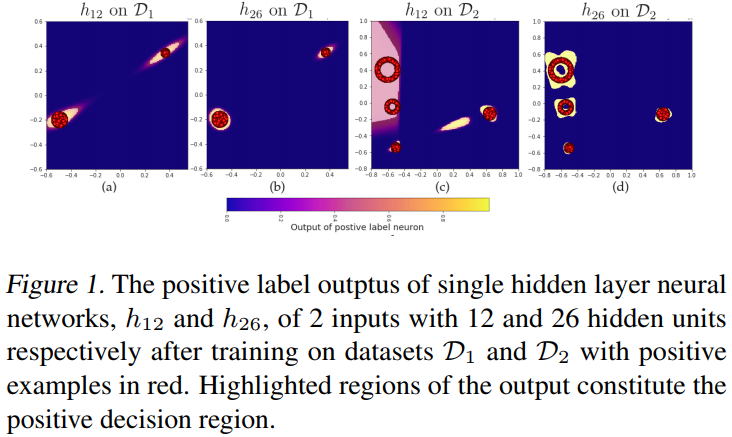
For example, in fig. 1, a MLP with 12 hidden neurons is not expressive enough to fit a ring (c), whereas 26 hidden neurons MLP can.

Topology

Basically, topology characterizes shapes by their connectivity. In topology, two sets are similar if there exists a continuous deformation (rotation, translation, etc) such that the sets become equal.

Furthermore, algebraic topology will characterize data with a measure of geometric complexity. For exemple, \(D_1\) as the following complexity : \(\{Z^2, 0 , 0\}\). The first dimension is the number of “0D” holes, the number of connected components, there is no ring and no “3D” hole.

\(H(D_2) = \{Z^4, Z^2, 0\}\), there are 4 connected components, two rings and no “3D” hole. Using this notation, we pose that \(D_2\) is harder than \(D_1\).

In this work, the authors use groups to describe “holes” in the data. Two sets are equivalent if the groups assigned are isomorphic.

Method

We pose \(B_i\) the number of holes of dimension \(i\). It’s called the Betti number.

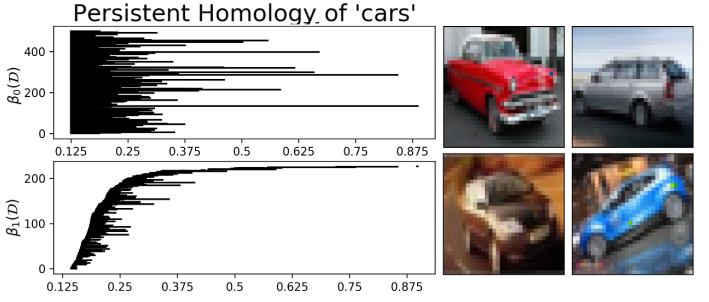
In practice, homology is computed with connected components. They compute it by increasing a radius \(\epsilon\) around each point. From the car class of CIFAR10, they first compute an embedding of the dataset (LLE with 120 neighbors). They then compute the homology for various \(\epsilon\).

They show there exist a loop in \(B_1(D)\) (between 0.625 and 0.82). They suppose that this loop is in relation with the rotation of the cars.

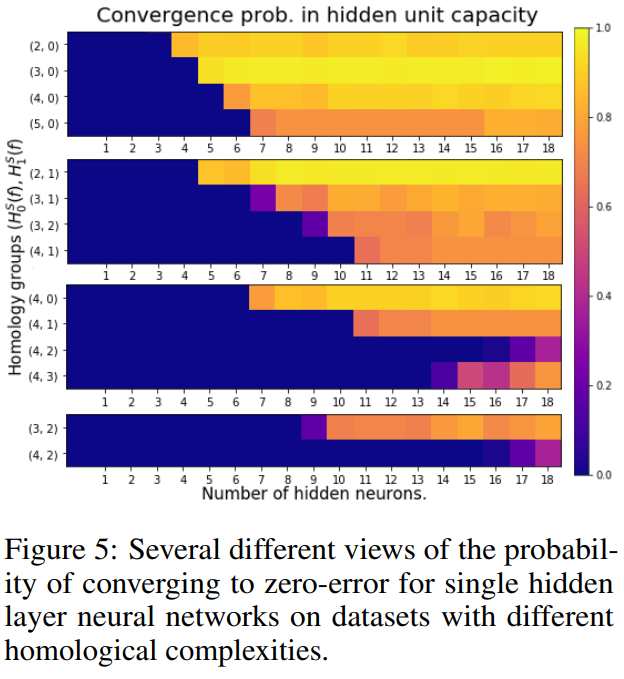
Furthermore, they show that the homological complexity is in relation with the number of neurons one would need to correctly approximate this function.